Bioimpacts. 2025;15:30596.
doi: 10.34172/bi.30596
Original Article
Stabilization of Hoogsteen H-bonds in G-quartet sheets by coordinated K+ ion for enhanced efficiency in guanine-rich DNA nanomotor
Abolfazl Barzegar Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing – review & editing, 1, 2, 3, * 
Nastaran Tohidifar Data curation, Formal analysis, Investigation, Writing – original draft, 2
Author information:
1Department of Biology, Faculty of Natural Sciences, University of Tabriz, Tabriz, Iran
2Research Center of Biosciences and Biotechnology (RCBB), University of Tabriz, Tabriz, Iran
3Department of Medical Biotechnology, Faculty of Advanced Medical Sciences, Tabriz University of Medical Sciences, Tabriz, Iran
Abstract
Introduction:
G-rich DNA nanomotors function as nanoscale devices and nanoswitches powered by the conversion of chemical energy into mechanical motion through transitions between duplex (DU) and tetraplex (TE) conformations. The stability of the TE conformation, crucial for nanomotor function, relies on G-quadruplex structures formed by guanine quartets. However, the detailed factors influencing TE stability remain unclear.
Methods:
This study investigated the role of coordinated K+ ion and Hoogsteen H-bonds in stabilizing the TE structure of a truncated 15-nucleotide G-rich DNA nanomotor with the sequence GGTTGGTGTGGTTGG using atomic-scale computational analysis. Three systems were simulated: TE1K with a crystal K+ ion, TE2K with a manually embedded K+ ion, and TE3 lacking a K+ ion. All systems underwent molecular dynamics simulations using the Amber force field and TIP3P water model.
Results:
The simulations revealed a clear dependence of G-quadruplex rigidity and TE conformation stability on the presence of coordinated K+ ion. TE1K and TE2K, containing K+ ions, exhibited significantly lower RMSD values compared to TE3, indicating more excellent structural stability and rigidity. K+ ion coordination facilitated the formation of all eight Hoogsteen H-bonds within G-quartets, whereas the K+ ion-free system (TE3) displayed distorted G-quadruplexes and a reduction in H-bonds, leading to a less stable "wobble TE*" state. The diameter of G-quartets and the radius of gyration (Rg) further supported these observations, with TE1K and TE2K maintaining compact structures compared to the more open and flexible "wobble TE*" conformation in TE3.
Conclusion:
These findings demonstrate that coordinated K+ ion play a critical role in stabilizing the TE conformation of G-rich DNA nanomotors by promoting G-quadruplex rigidity and facilitating Hoogsteen H-bond formation. This enhanced stability is essential for efficient DNA nanomotor function in the DU-TE nanoswitching process.
Keywords: DNA nanomotor, G-rich DNA, Tetraplex, G-quartet, MD simulation, Hoogsteen H-bonds
Copyright and License Information
© 2025 The Author(s).
This work is published by BioImpacts as an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (
http://creativecommons.org/licenses/by-nc/4.0/). Non-commercial uses of the work are permitted, provided the original work is properly cited.
Funding Statement
No specific funding was received for this research.
Introduction
A nanomotor is described as a nanoscale device generating a linear or a rotational motion at the molecular range, which is capable of converting energy into acceptable controlled movement.1,2 In consequence, using nanomotors makes the transportation of molecules or nanodevices possible. With advancements in nanotechnology, the demand for nanomotors has significantly increased due to their potential applications in powering nanoscale devices across various fields, including biosensors, gene therapy, drug delivery, nanoscale manufacturing, and the regulation of chemical reactions.3,4 These applications have been of interest by recent demonstrations of a group of nanomotor designs that use a variety of methods and constructions including; organic molecules,5 protein motors,6 inorganic/protein hybrids7 and engineered DNA constructs.8,9 Most of the protein motors including myosin, kinesin, and F0F1 adenosine triphosphate (ATP) synthase are more “complex systems” and make their mechanical movement by an ATPase activity. Therefore, significant effort has been devoted to the design and synthesis of "simple systems" for artificial nanomotors (devices that convert chemical energy into mechanical movement at the nanoscale). These systems aim to enhance efficiency, functionality, and adaptability for various applications.10 While most synthetic nanomotors have relied on small molecules, recent progress has expanded this field to include DNA-based nanomotors, which offer novel functionalities.11,12
DNA nanomotors are highly efficient molecular devices, offering cost-effective synthesis and compatibility with biological systems.13,14 These nanomotors exhibit remarkable structural flexibility, adopting diverse shapes and conformations that can be precisely controlled at the nanoscale.15,16 A previously reported guanine-rich (G-rich) 17-mer DNA nanomotor has demonstrated the ability to transition between two distinct conformational states: an intramolecular tetraplex (TE) and an intermolecular duplex (DU).8,13 The nanomotor transitions between these two conformations via alternating DNA hybridization and strand exchange reactions, which drive the inchworm-like extending and shrinking motion of the nanomotor as represented in Fig. 1 (DU < = = > TE). The self-associating properties of guanine in G-rich oligonucleotide strands leads to the formation of planar G-quadruplexes, where four guanines (G-quartets) are stabilized through eight hydrogen bonds (H-bonds).17,18 The coplanar G-quartets are well-defined conformations and are highly polymorphic resulting in TE nanomotor.19,20 Therefore, the DNA nanomotor requires the consistency of higher-order G-quadruplex conformations to operate.
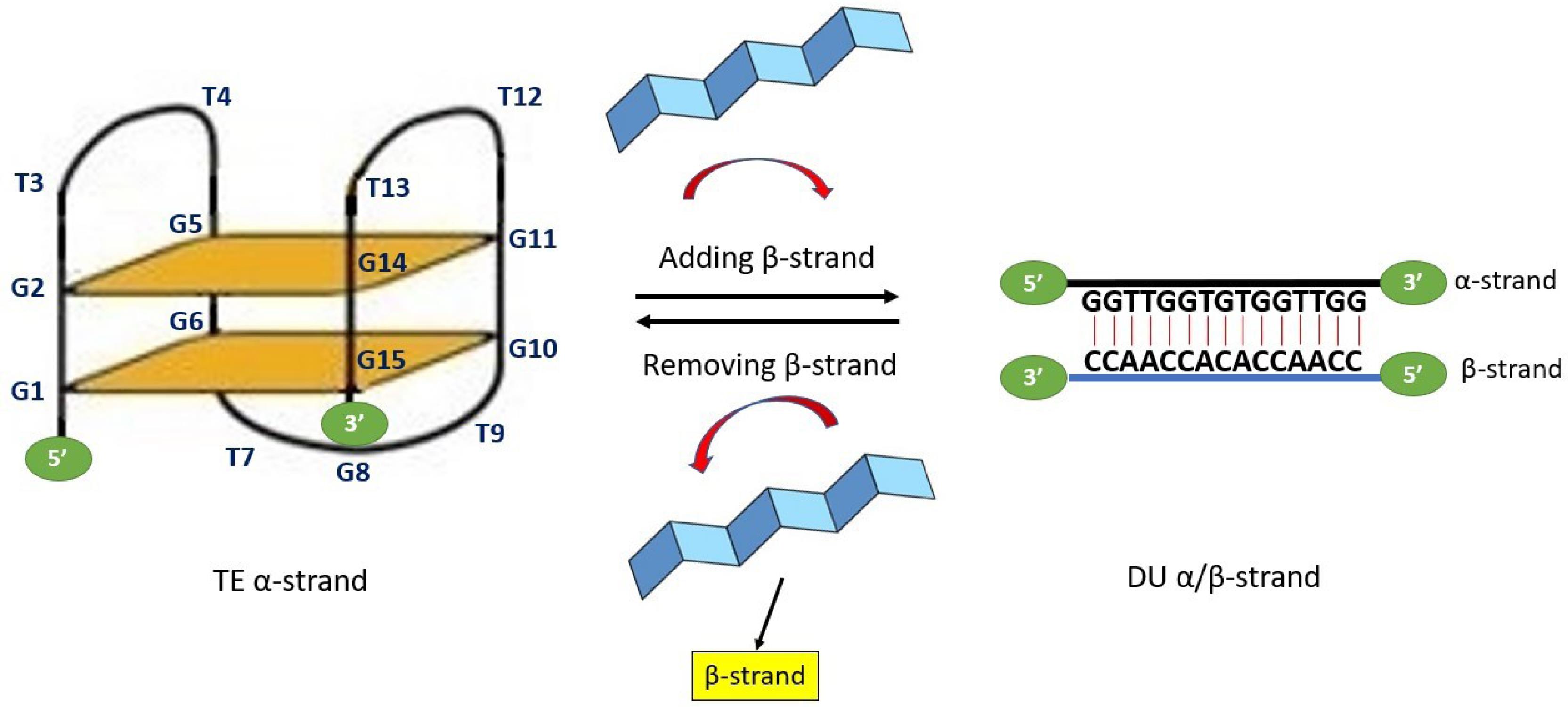
Fig. 1.
15mer α-strand DNA nanomotor (G1G2T3T4G5G6T7G8T9G10G11T12T13G14G15) can adopt an intramolecular tetraplex (TE) conformation. Two G-quadruplexes are presented in the TE conformation state as G-quartet 1 (G1G6G10G15) and G-quartet 2 (G2G5G11G14). Three lateral linker loops including loop-1 (T3T4), loop-2 (T12T13) and loop-3 (T7G8T9) are connecting strand and supporting the G-tetrad core in G-quartets. The nanomotor transitions into a duplex (DU) state upon hybridization with a complementary β-strand and reverts to its contracted form (TE) through the process of β-strand exchange or removal
.
15mer α-strand DNA nanomotor (G1G2T3T4G5G6T7G8T9G10G11T12T13G14G15) can adopt an intramolecular tetraplex (TE) conformation. Two G-quadruplexes are presented in the TE conformation state as G-quartet 1 (G1G6G10G15) and G-quartet 2 (G2G5G11G14). Three lateral linker loops including loop-1 (T3T4), loop-2 (T12T13) and loop-3 (T7G8T9) are connecting strand and supporting the G-tetrad core in G-quartets. The nanomotor transitions into a duplex (DU) state upon hybridization with a complementary β-strand and reverts to its contracted form (TE) through the process of β-strand exchange or removal
In this study, a previously synthesized and efficient 17-mer DNA nanomotor was truncated to a 15-mer variant (depicted in Fig. 1). Through atomic-scale computational analysis, we investigated the stability of the TE conformation, focusing on the G-quadruplex structure, which holds potential for applications in nanosystems. The advantages of the 15-mer G-rich DNA nanomotor in this investigation lie in its single strand DNA composition, small molecular weight, and the minimal number of G-quartets (two G-quartets) required to form the TE structure. We extensively explored the significance of a coordinated single K+ ion positioned between the planes of guanine-O6 quartets. This comprehensive investigation revealed the essential role played by this coordinated K+ ion in enhancing the stability of the TE conformation within the nanomotor structure.
Theoretical Methods
Initial G-rich TE nanomotor geometries
The G-rich TE nanomotors effectively convert noncovalent binding energies into mechanical force through an opening-closing process.15 We obtained primary coordinates for two different crystal structures of TE nanomotors from the Protein Data Bank (http://www.rcsb.org/). The used PDB codes for the 15-mer oligonucleotide G-rich TE nanomotor, with the sequence d(GGTTGGTGTGGTTGG), are 4DII (TE1K), containing a single K+ ion between the planes of neighboring G-quartets, and 1HUT (TE3), representing an ion-free conformation. Both 4DII (TE1K) and 1HUT (TE3) 15-mer nanomotors form intramolecular antiparallel G-quartets, as shown in Fig. S1 (Supplementary file 1).
To comprehensively study the role of the K+ ion in the action of the TE nanomotor, we manually embedded the crystal K+ ion between the planes of neighboring G-quartets in 1HUT. This was achieved by superimposing the coordinates of the K+ -bound conformation from 4DII onto the corresponding regions of 1HUT. This process involved aligning the structural features of 4DII to ensure that the K+ ion was accurately positioned to maintain the spatial integrity of the G-quartets. The resulting conformation, now containing the K+ ion, was designated TE2K (Fig. S1).
Force field
We considered the all-atom Amber parm99 force field parameters,21,22 for nucleobases into the following MD simulations. The standard Amber parm99 force field was modified by incorporating parameters from the developed parmbsc0 set,23 specifically tailored for G-quadruplex DNA structures.24 Notably, torsional parameters involving the α and γ torsions were refined to better model the interactions within the G-rich sequences. All other parameters were retained at their standard parm99 values.21 This modified force field not only accurately simulates the structural and dynamic properties of various nucleic acids but also provides reliable representations of G-quadruplex DNA structures.24
DNA simulations were seen to be particularly sensitive to the treatment of electrostatics. Early simulation approaches often neglected electrostatic interactions or limited them to short-range truncation, with typical cut-off distances around 10 Å. The implementation of techniques like the 'twin-range' cut-off allowed for the extension of these interactions to larger distances, such as 15 Å.25 Herein to account for long-range electrostatic interactions, the particle mesh Ewald (PME) algorithm was used with a cut-off 14 Å. This value is a widely accepted standard in molecular dynamics simulations, particularly for nucleic acid structures, which possess charged phosphate backbones. The selection of this cutoff was made to balance computational efficiency with the need for accurate representation of long-range interactions, ensuring that the majority of significant electrostatic interactions are captured while minimizing computational cost. While the 14 Å cutoff may limit the representation of some long-range interactions, we mitigated this by employing the PME method to treat long-range electrostatics more rigorously, thus enhancing the accuracy of the simulations without excessively increasing computational demands.
Molecular dynamics
Simulations provide a practical approach to addressing specific questions regarding the properties of a model system and the underlying biological mechanisms, often simplifying the investigation compared to experiments conducted on actual systems.26-28 Molecular dynamics (MD) simulations serve as an effective means of elucidating the conformational stability and atomic-scale orientations of G-quartets. For MD simulation we applied three systems including TE1K, TE2K and TE3. Both of TE1K and TE2K have single crystal K+ ion between the G-quartets that related to 4DII and manually embedded K+ ion in 1HUT, respectively. The system TE3 is ion-free structure that related to 1HUT. The structures of TE1K, TE2K, and TE3 were individually enclosed in a periodic box filled with water molecules, modeled using the equilibrated TIP3P (three-point charge) potential. The systems were placed in the center of the simulation boxes (Fig. S2) with the number of explicit water molecules 5165, 3235, and 3236 for TE1K, TE2K, and TE3, respectively. To neutralize the negative charge on the DNA backbone, additional positively charged K+ ions (13 K+ for TE1K and TE2K, and 14 K+ for TE3) were incorporated into the systems as represented in Fig. S2. The cations were initially placed into the most negative locations of the electrostatic potential using Coulombic potential terms with the LEAP module of Amber. To minimize the energy of each system and relax the solvent molecules, a steepest-descent algorithm was employed. MD simulations for each system were conducted in two stages, with a 2 fs integration time step. In the first stage, a position-restrained simulation was performed, wherein the DNA molecule's atoms were fixed while allowing the solvent molecules to move freely to achieve equilibrium. The second stage involved simulating each system for a total of 15 million steps. During the simulations, the Berendsen coupling algorithm was employed to maintain constant pressure and temperature conditions across all components. By weakly coupling the system to an external thermal bath, the algorithm ensures that deviations from the target temperature are corrected through velocity rescaling, enabling the system to reach the target temperature exponentially. The coupling parameter controls the speed of this adjustment, ensuring efficient temperature regulation. Although it does not rigorously reproduce the temperature fluctuations typical of canonical or isothermal-isobaric ensembles, the Berendsen algorithm is highly efficient and well-suited for large systems, especially during initial equilibration, providing smooth convergence with minimal computational cost.29 All simulations were performed using the Gromacs 5.0.4 software package.
Results and Discussion
G-quartets’ rigidity dependency on coordinate K+ ion
The more increased G-quadruplex structures rigidity, the more improved nanomotor efficiency by forming the stable TE conformation in extending-shrinking motion, DU < = = > TE switching (Fig. 1).13 The root mean-square deviation (RMSD) was calculated throughout the simulation to assess the conformational equilibration of the system.26,28 The RMSD values for the atoms of 15-mer DNA nanomotors were shown in Fig. 2. The total RMSD values are equilibrated after 10 000 ps simulation, which means almost all systems are stable and maintaining TE conformation. Additionally, it shows that the sequential stability of the TE conformation is TE1K > TE2K > TE3. The crystal ion-free conformation, TE3, exhibited a significant increase in RMSD value, approximately 0.5 nm, whereas the RMSD value for the conformation with the crystal ion, TE2K, remained around 0.3 nm. This suggests that the absence of the K+ cation leads to structural rearrangement and instability in the higher-order G-quadruplex. Also, the RMSD value in TE1K with crystal ion, is fluctuated and relaxed around ~0.2 nm after 10 000 ps simulation meaning the high stability of TE1K. These findings about the role of K+ in keeping the higher-order G-quadruplex structures are also obvious by separately analyzing the RMSD values of G-quartets 1 and 2. Both G-quartets are highly rigid with the minimum RMSD value for TE1K (RMSDmean < 0.1 nm). Moreover, adding K+ in the core of G-quartets caused decreasing of RMSD values in TE2K comparing with RMSD values of TE3. Please note the almost similarity among RMSD of loop-1, loop-2 and loop-3 in all three systems of TE1K, TE2K, and TE3. This observation suggests that the predominant contributors to the total RMSD in all three systems are the orientations and rearrangements of G-quartet 1 and G-quartet 2. This observation suggests that the predominant contributors to the total RMSD in all three systems are the orientations and rearrangements of G-quartet 1 and G-quartet 2.
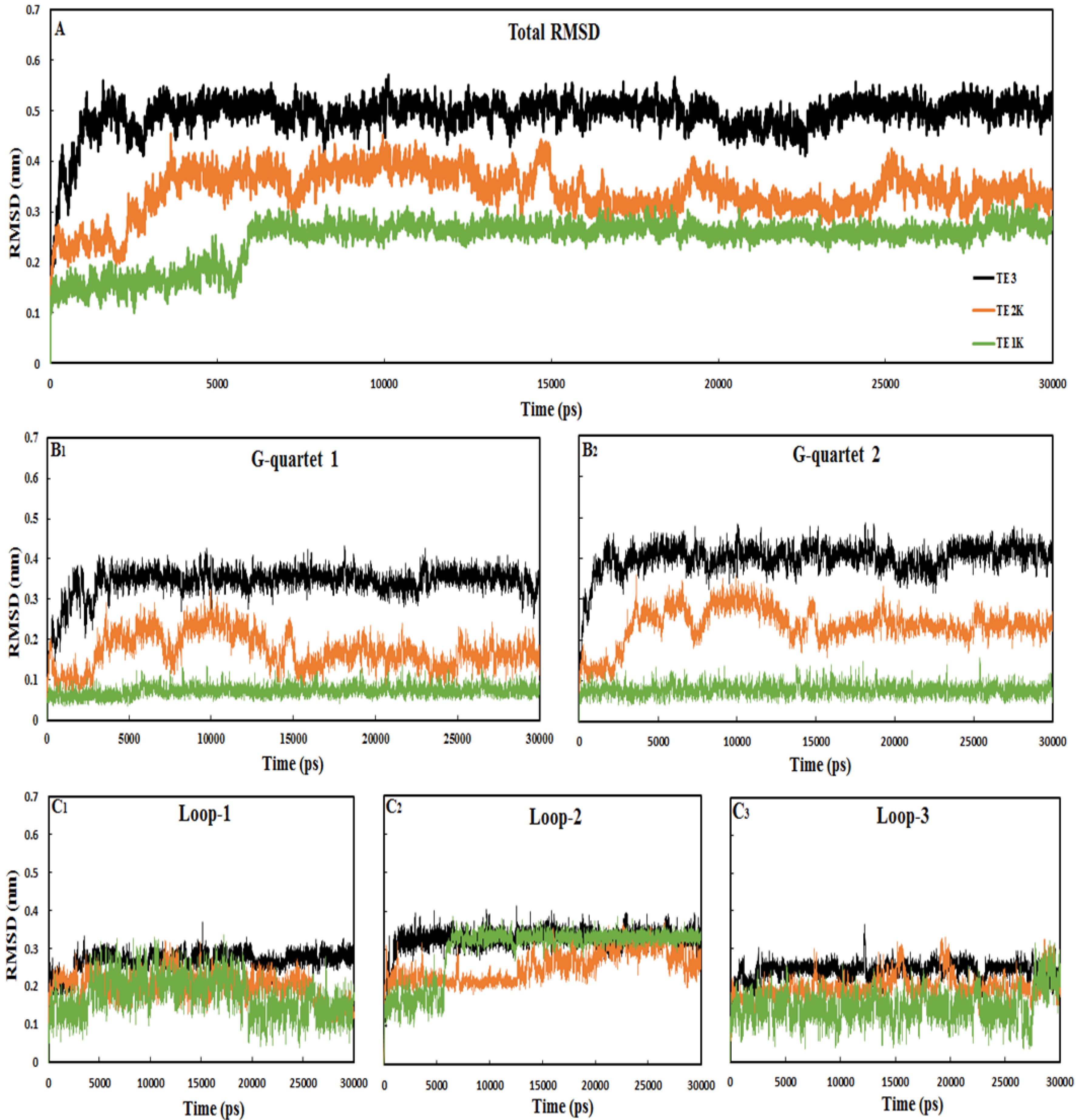
Fig. 2.
RMSD analysis of the 15-mer DNA nanomotors TE1K, TE2K and TE3 during 30,000 ps dynamics runs. A; total RMSD of the systems, B; RMSD values for G-quartets 1 and 2, C; RMSD for loop-1, loop-2 and loop-3. Further details regarding the quartets and loops can be found in Fig. 1. All systems reached equilibrium during the 30 000 ps MD simulations
.
RMSD analysis of the 15-mer DNA nanomotors TE1K, TE2K and TE3 during 30,000 ps dynamics runs. A; total RMSD of the systems, B; RMSD values for G-quartets 1 and 2, C; RMSD for loop-1, loop-2 and loop-3. Further details regarding the quartets and loops can be found in Fig. 1. All systems reached equilibrium during the 30 000 ps MD simulations
Upon the addition of a coordinated ion in TE2K, the system demonstrates improved stability in the tetraplex conformation, with RMSD values that align more closely with those of TE1K (with crystal ion at the core of the G-quartets). However, all systems exhibit flexibility in the loop regions, particularly in the TE1K and TE2K configurations. Therefore, the stability of 15-mer nanomotor structure is correlated in G-quadruplex conformational rigidity under coordinated K+ ion. It can be proposed that the 15-mer G-rich DNA needs K+ ion to induce a “compact rigid TE” state. Thermal energy can destabilize the higher-order G-quadruplex structure without K+ ions resulting in a less stable “wobble flexible TE” conformation. The importance and stability of the G-quadruplex structure in inducing compact or wobble TE conformations were assessed through: a) examining the interaction between guanine-O6 carbonyl groups and K+ ion, b) quantifying the number of Hoogsteen hydrogen bonds, and c) analyzing the diameter of G-quartets and the radius of gyration (Rg) values of the TE structures (as discussed in the following sections).
Coordinated K+ preserves high-order G-quadruplex compactness
The formation and stabilization of G-quadruplexes,30 alternative DNA structural motifs, are considered not only to be functionally important in the biological point of view such as genome stability but also in nanotechnology making the DNA nanomotor practically useful for powering nanosystems’ application. G-quadruplex stability relies on monovalent cations, particularly K+ and Na +, which position themselves within the core of G-quartets formed by the coplanar arrangement of four guanines.31-33 The K+ cation is attached to guanine-O6 carbonyl groups between the neighboring G-quartet that is represented in Fig. S3. The G-quadruplexes are mainly stabilized by cyclic Hoogsteen H-bonding between 4 guanines, forming G-quartets in the presence of monovalent metal ions especially K+.34,35 As indicated in Fig. S3 the G-quartet is coordinated and stabilized by the association of K+ with four guanine O6 carbonyl groups, resulting in the formation of 8 Hoogsteen H-bonds between the O6… (NH)1 and N7… (NH)2 groups. Therefore, in the presence of K+, G-quartets readily form quadruplex structures. Experimental stability assessment of telomeric G-quadruplexes revealed the favorable stability of TE structure in the presence of potassium.35,36 The K+ ion is well preserved in the G-quadruplexes structures of TE1K and TE2K through simulations as indicates in Fig. 3 with visual inspection. It shows that the coordination of K+ ion in the core of G-quartet 1 and G-quartet 2 is constant with strong interactions in TE1K (see guanine-O6----K+ distances). Almost similar results were achieved for TE2K instead of some distortion in G-quartet 2. Nevertheless, both of G-quartets 1 and 2 are distorted in crystal ion-free TE3 system. Each G-quartet sheet contains a number of four G nucleotides in the short space, thus, the steric hindrance between adjacent four guanine-O6 carbonyl groups caused to distort the G-quartet sheets in TE3. The coordinated ion situated between guanines in the G-quadruplex helps mitigate repulsive forces between the O6 atoms, resulting in a more compact and stable TE conformation. Visual inspection of different snapshots of TE1K, TE2K and TE3 in Fig. S4- Fig. S6, indicates the importance of crystal K+ ion in the compactness of TE structures. The K+ cation is coordinated to guanine-O6 carbonyl groups between the planes of neighboring quartets in all snapshots of TE1K and TE2K. It is evident that the tetraplex structures in TE1K and almost in TE2K remain intact during simulation meaning quartet-ion interaction plays a significant role in the stabilization of the G-quadruplex structures resulted in compact tetraplex state. In free-ion TE3 system, the TE conformation was almost changed and the compactness decreased throughout simulation (see snapshots in Fig. S6). We emphasize the particular state of TE in ion-free state for the 15-mer G-rich DNA as “wobble TE” state. Folding of a G-rich oligonucleotide into an intramolecular G-quartets leads to a compact structure stabilized by K+ in TE1K and TE2K. Fig. S4-Fig. S6 indicate that the neutralized K+ ions are unable to enter in G-quartets’ core while the coordinated crystal K+ ion is well preserved in the structures TE1K and TE2K during MD simulations. Similar results about neutralized ions were achieved for sodium, Na + (data not shown). It is obvious to conclude that the behavior of solution K+ ion is entirely different from crystal ion.

Fig. 3.
The G-quadruplexes conformations in TE1K, TE2K and TE3. The K+ cation is attached and maintained to guanine-O6 carbonyl groups between the planes of neighboring quartets of TE1K, TE2K. The Hoogsteen H-bonds and coordinated K+ in initial step and after 30 ns MD simulations are separately presented for quartet 1 and quartet 2
.
The G-quadruplexes conformations in TE1K, TE2K and TE3. The K+ cation is attached and maintained to guanine-O6 carbonyl groups between the planes of neighboring quartets of TE1K, TE2K. The Hoogsteen H-bonds and coordinated K+ in initial step and after 30 ns MD simulations are separately presented for quartet 1 and quartet 2
Coordinated K+ ion induces Hoogsteen H-bonds consistency
The stability of the quadruplex structures in TE1K, TE2K, and TE3 was evaluated by monitoring changes in Hoogsteen hydrogen bonds during MD simulations. These bonds, formed between O6…H1-N1 and N7…H2-N2 groups, are crucial for maintaining the G-quadruplex structure and provide insight into the conformational integrity of the system (see Fig. S3 and Fig. 3). The strength of these Hoogsteen H-bonds is the primary force promoting G-quadruplex stability. The formation of hydrogen bonds in G-quartets 1 and 2 was tracked throughout the simulation, as shown in Fig. 4. The average H-bond occupancy in G-quartet 1 for TE1K, TE2K, and TE3 was 8.6, 7.6, and 5.3, respectively, while in G-quartet 2, the occupancies were 7.9, 6.4, and 3.6, respectively. In TE1K, all eight Hoogsteen hydrogen bonds remained consistently intact in both G-quartets, resulting in a compact and stable tetraplex configuration. However, in TE3, due to the absence of the crystal ion, several Hoogsteen H-bonds were lost, particularly in G-quartet 2, leading to a reduction in the overall stacked stability of the G-quadruplex. As shown in Fig. 3, steric hindrance caused the distortion of G-quartet sheets, leading to the displacement of the 2-amino groups from the core of the G-tetrads. This disruption impaired the planar stacking of the G-quartets, breaking some Hoogsteen H-bonds and leading to the formation of bifurcated hydrogen bonds, thereby contributing to the wobble TE structure. In contrast, the coordinated K+ ion in TE2K supported the establishment of Hoogsteen bonds similar to those in TE1K, ensuring consistent H-bond formation. The presence of the K+ ion within the core of the G-quartets reinforced structural stability, maintaining the high-order G-quadruplex conformation.
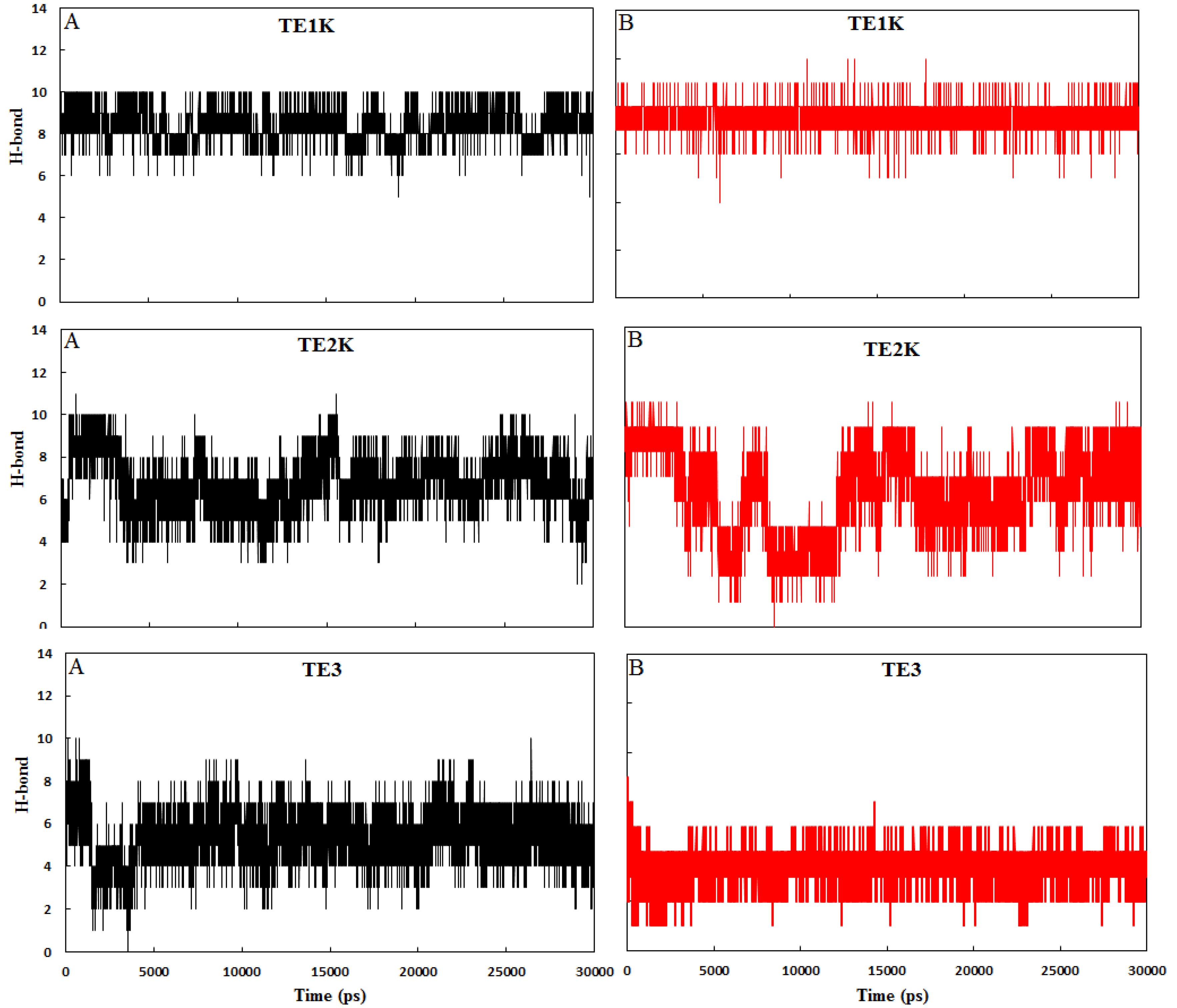
Fig. 4.
The number of H-bonds for G-qurtet 1 (A) and G-quartet 2 (B) in TE1K, TE2K and TE3 complexes as a function of simulation times
.
The number of H-bonds for G-qurtet 1 (A) and G-quartet 2 (B) in TE1K, TE2K and TE3 complexes as a function of simulation times
To further investigate the role of hydrogen bonding in stabilizing the TE1K, TE2K, and TE3 structures, the intra- and intermolecular hydrogen bonding networks were also analyzed using the HBAT 1.1 program.37 This tool facilitated a detailed evaluation of hydrogen bond interactions within the molecular structures and between the structures and surrounding solvent molecules. The HBAT analysis applied default parameters, with bond angles ranging from 90° to 180° and distances between 1.2 Å and 3.2 Å. As presented in Table 1, TE3 exhibited a greater number of hydrogen bonds in both intramolecular (N-H...O, N-H...N) and intermolecular (TE3-H2O) interactions, including N-H...O and O-H...N bonds. These findings suggest that in the absence of the K+ ion, the Hoogsteen bond network in TE3 undergoes substantial rearrangement, forming new hydrogen bonds, particularly with water molecules. The additional intermolecular and intramolecular hydrogen bonds in TE3 may disrupt the native Hoogsteen bond pattern, undermining G-quadruplex stability and promoting the wobble conformation of the G-tetrads.
Table 1.
Hydrogen bond profiles in TE1K, TE2K, and TE3 systems
|
System
|
N-H...O
|
N-H...N
|
O-H...N
|
Total
|
| TE1K |
11.8 |
12 |
- |
23.8 |
| TE1K-H2O |
23.2 |
- |
27 |
50.2 |
| TE2K |
16.4 |
7.6 |
- |
24 |
| TE2K-H2O |
20.7 |
- |
28.3 |
49 |
| TE3 |
17 |
12.8 |
- |
29.8 |
| TE3-H2O |
27.25 |
- |
27.75 |
55 |
Note: Intra- and intermolecular hydrogen bond types (NH···N, OH···N, and NH···O) were quantified using HBAT 1.1. Distinctions include intramolecular (within DNA) and intermolecular (DNAwater) interactions based on distanceangle criteria from optimized structural models.
Conversely, TE1K and TE2K exhibited a similar hydrogen bonding network, further supporting the stabilizing role of the K+ ion in these structures by preserving the consistency of Hoogsteen hydrogen bonds and maintaining the G-quadruplex configuration. These findings underscore the critical role of the core K+ ion in stabilizing G-quadruplex structures by sustaining the integrity of Hoogsteen hydrogen bonds, thus reinforcing the structural order and stability of the quadruplex.
Compact/wobble TE by G-quartets’ diameter and Rg assessment
The diagonal diameter distance (Ddis) changes in G-quartet planes were evaluated to discover the compactness of G-quadruplex in TE structure. Fig. 5 shows that the Ddis values of G-quartets 1 and 2 in TE1K stay very constant in the whole simulation. Almost similar results were achieved for TE2K but the Ddis values were increased in TE3. The increased quartets’ diagonal diameter distance in TE3 is because of augmentation distances in the same direction of quartet 1 and quartet 2 between G6-G15 and mainly G5-G14 (see Figs. 1 and 5). Maximum compactness in TE is derived from the high-ordered G-quadruplex structures with the consistency of G-quartet sheets’ size. Any changes in G-quartets’ size and G-quadruplex’s order could be resulted in wobble TE conformers with smaller radius of gyration (Rg) as represented in Fig. 6. The radius of gyration shows the global shape of systems during the simulation. This figure indicates that TE1K and TE2K stay at nearly the same proportions during the simulation with a radius of gyration of 0.95-1 nm. It should be noted that tetraplex structures in TE1K and TE2K are cubic-like shape but increasing Ddis in TE3 resulted in globular coil-like (wobble tetraplex) as monitored in Fig. S4-S6. Therefore, TE3 has smaller Rg than TE1K and TE2K because of deflection of rectangular quartet sheets in TE3. Hence, the wobble TE conformation is accompanying with decreased Rg and augmented Ddis values.
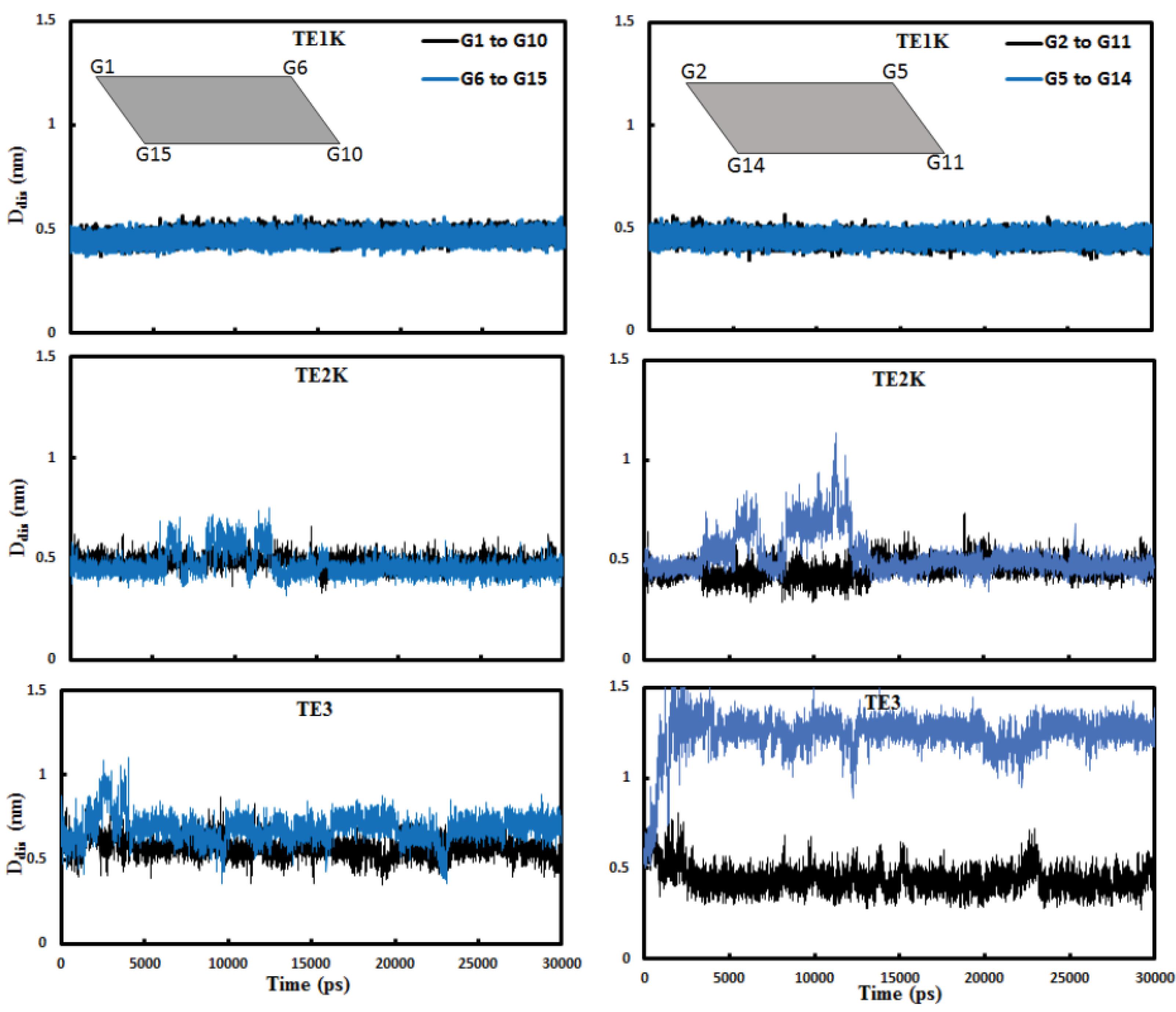
Fig. 5.
The diagonal diameter distance (Ddis) changes in “G-quartet 1” (left panels) and G-quartet 2 (right panels) in 15-mer DNA nanomotors of TE1K, TE2K and TE3 during 30 000 ps.
.
The diagonal diameter distance (Ddis) changes in “G-quartet 1” (left panels) and G-quartet 2 (right panels) in 15-mer DNA nanomotors of TE1K, TE2K and TE3 during 30 000 ps.
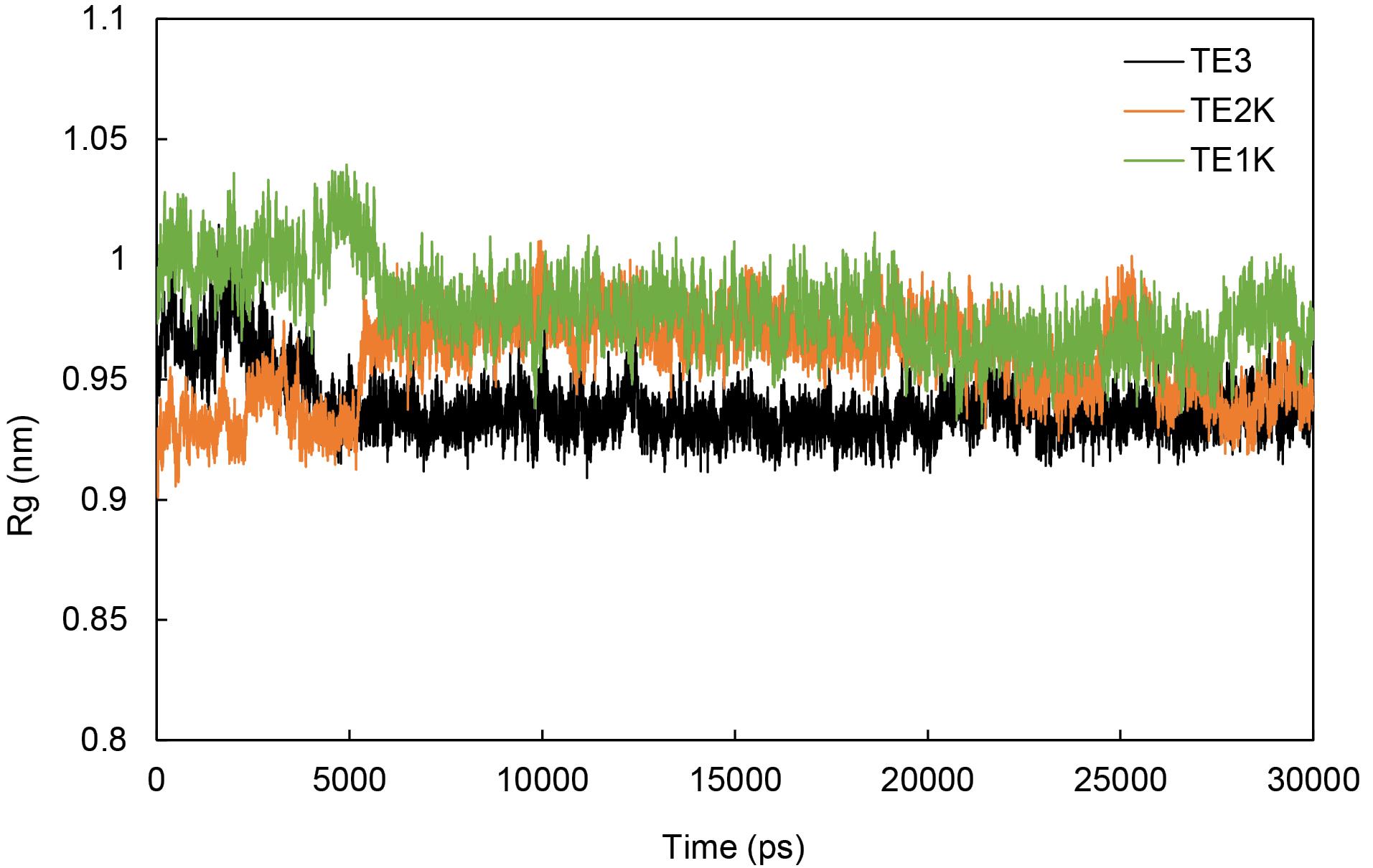
Fig. 6.
Plot of the radius of gyration during the simulation of TE1K, TE2K and TE3.
.
Plot of the radius of gyration during the simulation of TE1K, TE2K and TE3.
The efficiency of DNA nanomotor dependency on compact TE
The mechanical force for G-rich 17-mer oligonucleotide of DNA nanomotor with DU and TE formation possibility was calculated to be 20.7 pN (~10 times larger than kinesin/myosin forces) in switching between DU and TE conformations.38 This remarkable property of G-rich DNA nanomotor is because of the unusual structures of high-ordered G-quadruplexes containing coplanar G-quartets.13 So, the mechanical efficiency of G-rich 15-mer DNA nanomotor depends on the energy changes between TE < = = > DU switching conformation (extending-shrinking motion). This energy is directly changed by changing the critical conformation of TE or DU. This property is illustrated in Fig. 7, where any alterations in the higher-order G-quadruplex structure indicate a disordered TE state, leading to the formation of the wobble TE* intermediate. The disordering state of TE is accompanying with losing some Hoogsteen hydrogen bonds, increasing Ddis, decreasing Rg. All of them are affected from coordinated monovalent K+ ion.
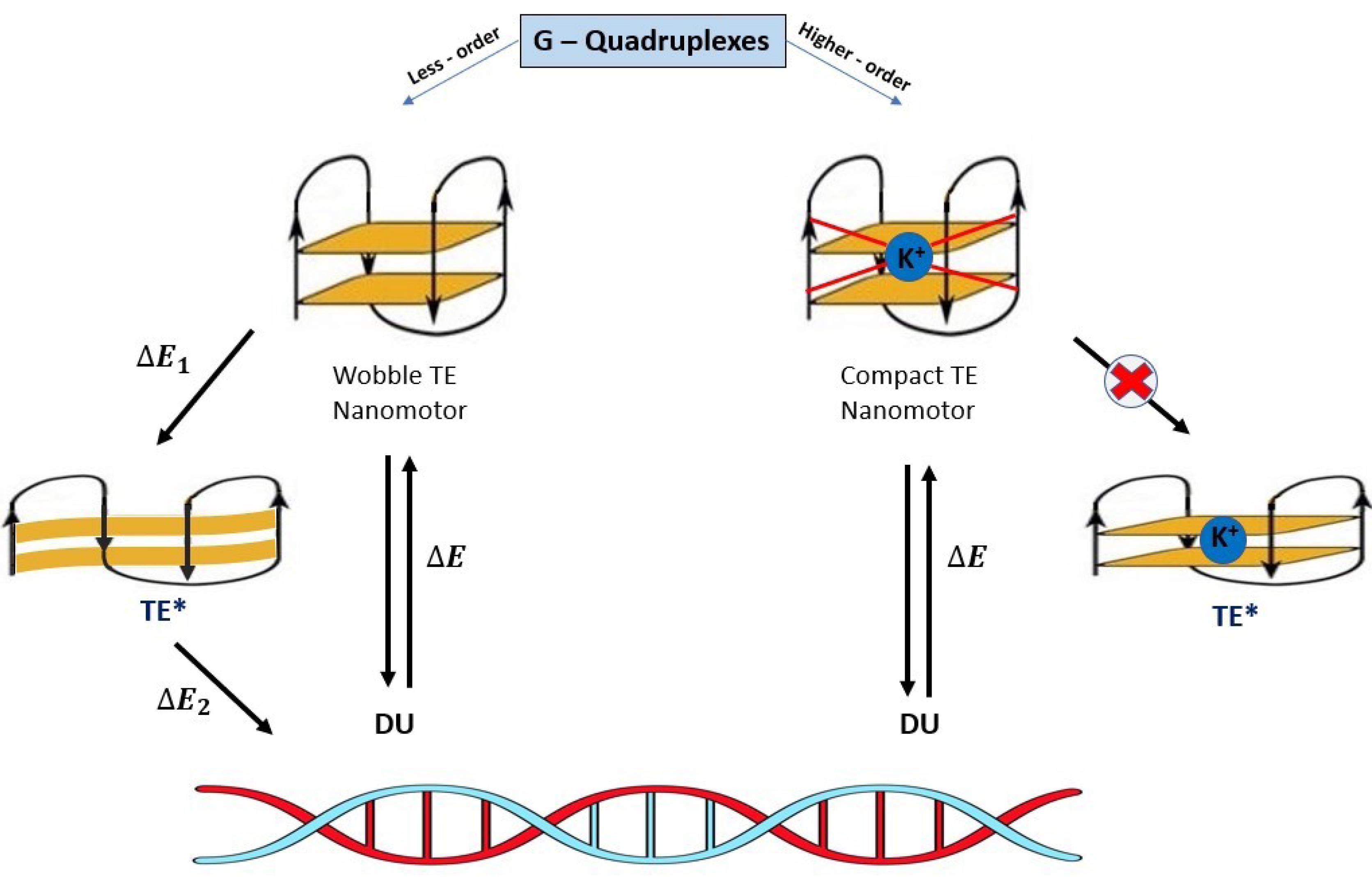
Fig. 7.
Schematic representation of G-rich 15-mer DNA nanomotor efficiency (W) dependence on the energy changes ΔE between TE < = = > DU exchanging conformation. The ion-free TE conformer is shifting to TE* intermediate results in decreasing the nanomotor efficiency by splitting ΔEtot into ΔE1 and ΔE2 (W = ΔE2 then W < ΔEtot). The value of ΔE1 is useless energy in nanomotor operating system denote the TE* as a waste product of TE. The coordinated monovalent K+ ion highly increases the nanomotor operating system (W ≈ ΔEtot).
.
Schematic representation of G-rich 15-mer DNA nanomotor efficiency (W) dependence on the energy changes ΔE between TE < = = > DU exchanging conformation. The ion-free TE conformer is shifting to TE* intermediate results in decreasing the nanomotor efficiency by splitting ΔEtot into ΔE1 and ΔE2 (W = ΔE2 then W < ΔEtot). The value of ΔE1 is useless energy in nanomotor operating system denote the TE* as a waste product of TE. The coordinated monovalent K+ ion highly increases the nanomotor operating system (W ≈ ΔEtot).
Consequently, the stability of TE conformation with high-ordered quadruplexes in G-rich nanomotors is essential in converting chemical energy to mechanical work by producing twisting or opening-closing movements. Disordering in G-quadruplex causes less efficiency of DNA nanomotor in DU < = = > TE process. The stability of the TE conformation arises from the intrinsic Hoogsteen hydrogen bonds and the external coordination of the K+ cation within the central channel of the stacked G-tetrads.
Conclusion
The stability of G-quadruplex structures in G-rich DNA nanomotors is essential for the design and utilization of these molecular nanomotors in nanotechnology. G-quadruplexes are 3-D structures formed in nucleic acids by sequences rich in guanine. Different TE modes and the stability of G-quadruplexes structure in a guanine-rich 15-mer DNA nanomotor have been systematically investigated through MD simulations. It was clearly shown that the ion-free system prefers to form wobble TE* structures with G-quadruplex distorting and attenuating intrinsic Hoogsteen H-bonds. Also, the action of solution countourion K+ is entirely different from crystal ion that cannot spontaneously moves into the central core of the quartets.
Research Highlights
What is the current knowledge?
What is new here?
-
The study theoretically investigates the stabilization of Hoogsteen H-bonds by coordinated K + ions in a 15-mer G-rich DNA nanomotor.
-
It demonstrates that coordinated K + ions transition the wobble TE state to a more stable compact TE state.
Competing Interests
The authors declare no conflicts of interest related to this paper.
Ethical Approval
There is none to be disclosed.
Supplementary files
Supplementary file 1 includes Figs. S1-S6.
(pdf)
Acknowledgements
This work was supported by the University of Tabriz, whose support is gratefully acknowledged. The authors also extend their appreciation to S. Moosavi for assisting in curating some of the molecular dynamics data.
References
-
Chowdhury D. Molecular motors: design, mechanism, and control. Comput Sci Eng 2008. 10: 70-7. doi: 10.1109/mcse.2008.58.
- Singhania A, Kalita S, Chettri P, Ghosh S. Accounts of applied molecular rotors and rotary motors: recent advances. Nanoscale Adv 2023; 5:3177-208. doi: 10.1039/d3na00010a [Crossref] [ Google Scholar]
- Craighead HG. Nanoelectromechanical systems. Science 2000; 290:1532-6. doi: 10.1126/science.290.5496.1532 [Crossref] [ Google Scholar]
- Pitikultham P, Wang Z, Wang Y, Shang Y, Jiang Q, Ding B. Stimuli-responsive DNA origami nanodevices and their biological applications. ChemMedChem 2022; 17:e202100635. doi: 10.1002/cmdc.202100635 [Crossref] [ Google Scholar]
- Yan M, Liang K, Zhao D, Kong B. Core-shell structured micro-nanomotors: construction, shell functionalization, applications, and perspectives. Small 2022; 18:e2102887. doi: 10.1002/smll.202102887 [Crossref] [ Google Scholar]
- Hoersch D. Engineering a light-controlled F1 ATPase using structure-based protein design. PeerJ 2016; 4:e2286. doi: 10.7717/peerj.2286 [Crossref] [ Google Scholar]
- Soong RK, Bachand GD, Neves HP, Olkhovets AG, Craighead HG, Montemagno CD. Powering an inorganic nanodevice with a biomolecular motor. Science 2000; 290:1555-8. doi: 10.1126/science.290.5496.1555 [Crossref] [ Google Scholar]
- Alberti P, Mergny JL. DNA duplex-quadruplex exchange as the basis for a nanomolecular machine. Proc Natl Acad Sci U S A 2003; 100:1569-73. doi: 10.1073/pnas.0335459100 [Crossref] [ Google Scholar]
- Ma J, Bai W, Zheng J. A novel self-cleaning electrochemical biosensor integrating copper porphyrin-derived metal-organic framework nanofilms, G-quadruplex, and DNA nanomotors for achieving cyclic detection of lead ions. Biosens Bioelectron 2022; 197:113801. doi: 10.1016/j.bios.2021.113801 [Crossref] [ Google Scholar]
- Wang L, Hao X, Gao Z, Yang Z, Long Y, Luo M. Artificial nanomotors: fabrication, locomotion characterization, motion manipulation, and biomedical applications. Interdisciplinary Materials 2022; 1:256-80. doi: 10.1002/idm2.12021 [Crossref] [ Google Scholar]
- Mao X, Liu M, Li Q, Fan C, Zuo X. DNA-based molecular machines. JACS Au 2022; 2:2381-99. doi: 10.1021/jacsau.2c00292 [Crossref] [ Google Scholar]
- Barzegar A, Moosavi S. Tetraplex structural stability of guanine-rich 15-mer DNA nanomotor based on the formation of higher-order G-quadruplex by consistent Hoogsteen H-bonds. Curr Nanosci 2017; 13:79-83. doi: 10.2174/1573413712666160720110526 [Crossref] [ Google Scholar]
- Li JJ, Tan W. A single DNA molecule nanomotor. Nano Lett 2002; 2:315-8. doi: 10.1021/nl015713+ [Crossref] [ Google Scholar]
- Li Y, Zhang C, Tian C, Mao C. A nanomotor involves a metastable, left-handed DNA duplex. Org Biomol Chem 2014; 12:2543-6. doi: 10.1039/c4ob00317a [Crossref] [ Google Scholar]
-
Kanatani K, Ochi Y, Okamoto A, Saito I. DNA nanomotor using duplex-quadruplex conformational transition. Nucleic Acids Res Suppl 2003; 161-2. doi: 10.1093/nass/3.1.161.
- Yin F, Mao X, Li M, Zuo X. Stimuli-responsive DNA-switchable biointerfaces. Langmuir 2018; 34:15055-68. doi: 10.1021/acs.langmuir.8b02185 [Crossref] [ Google Scholar]
- Doluca O, Withers JM, Filichev VV. Molecular Engineering of Guanine-Rich Sequences: Z-DNA, DNA Triplexes, and G-Quadruplexes. Chem Rev 2013; 113:044-3083. doi: 10.1021/cr300225q [Crossref] [ Google Scholar]
- Liu M, Pan L, Piao H, Sun H, Huang X, Peng C. Magnetically actuated wormlike nanomotors for controlled cargo release. ACS Appl Mater Interfaces 2015; 7:26017-21. doi: 10.1021/acsami.5b08946 [Crossref] [ Google Scholar]
- Batalia MA, Protozanova E, Macgregor RB, Erie DA. Self-assembly of frayed wires and frayed-wire networks: nanoconstruction with multistranded DNA. Nano Lett 2002; 2:269-74. doi: 10.1021/nl015672h [Crossref] [ Google Scholar]
-
Wang ZG, Ding B. Mechanical DNA devices. In: Kjems J, Ferapontova E, Gothelf KV, eds. Nucleic Acid Nanotechnology. Berlin, Heidelberg: Springer; 2014. p. 201-42. doi: 10.1007/978-3-642-38815-6_8.
- Krepl M, Zgarbová M, Stadlbauer P, Otyepka M, Banáš P, Koča J. Reference simulations of noncanonical nucleic acids with different χ variants of the AMBER force field: quadruplex DNA, quadruplex RNA and Z-DNA. J Chem Theory Comput 2012; 8:2506-20. doi: 10.1021/ct300275s [Crossref] [ Google Scholar]
- Rebič M, Mocci F, Laaksonen A, Uličný J. Multiscale simulations of human telomeric G-quadruplex DNA. J Phys Chem B 2015; 119:105-13. doi: 10.1021/jp5103274 [Crossref] [ Google Scholar]
- Pérez A, Marchán I, Svozil D, Sponer J, Cheatham TE 3rd, Laughton CA. Refinement of the AMBER force field for nucleic acids: improving the description of alpha/gamma conformers. Biophys J 2007; 92:3817-29. doi: 10.1529/biophysj.106.097782 [Crossref] [ Google Scholar]
- Moraca F, Amato J, Ortuso F, Artese A, Pagano B, Novellino E. Ligand binding to telomeric G-quadruplex DNA investigated by funnel-metadynamics simulations. Proc Natl Acad Sci U S A 2017; 114:E2136-45. doi: 10.1073/pnas.1612627114 [Crossref] [ Google Scholar]
- Darden T, Perera L, Li L, Pedersen L. New tricks for modelers from the crystallography toolkit: the particle mesh Ewald algorithm and its use in nucleic acid simulations. Structure 1999; 7:R55-60. doi: 10.1016/s0969-2126(99)80033-1 [Crossref] [ Google Scholar]
- Andarzi Gargari S, Barzegar A. Simulations on the dual effects of flavonoids as suppressors of Aβ42 fibrillogenesis and destabilizers of mature fibrils. Sci Rep 2020; 10:16636. doi: 10.1038/s41598-020-72734-9 [Crossref] [ Google Scholar]
- Rasafar N, Barzegar A, Mehdizadeh Aghdam E. Design and development of high affinity dual anticancer peptide-inhibitors against p53-MDM2/X interaction. Life Sci 2020; 245:117358. doi: 10.1016/j.lfs.2020.117358 [Crossref] [ Google Scholar]
- Rasafar N, Barzegar A, Mehdizadeh Aghdam E. Structure-based designing efficient peptides based on p53 binding site residues to disrupt p53-MDM2/X interaction. Sci Rep 2020; 10:11449. doi: 10.1038/s41598-020-67510-8 [Crossref] [ Google Scholar]
-
Zhou K, Liu B. Control techniques of molecular dynamics simulation. In: Zhou K, Liu B, eds. Molecular Dynamics Simulation. Amsterdam: Elsevier; 2022. p. 67-96. doi: 10.1016/b978-0-12-816419-8.00008-8.
- Varshney D, Spiegel J, Zyner K, Tannahill D, Balasubramanian S. The regulation and functions of DNA and RNA G-quadruplexes. Nat Rev Mol Cell Biol 2020; 21:459-74. doi: 10.1038/s41580-020-0236-x [Crossref] [ Google Scholar]
- Williamson JR, Raghuraman MK, Cech TR. Monovalent cation-induced structure of telomeric DNA: the G-quartet model. Cell 1989; 59:871-80. doi: 10.1016/0092-8674(89)90610-7 [Crossref] [ Google Scholar]
- Miura T, Benevides JM, Thomas GJ Jr. A phase diagram for sodium and potassium ion control of polymorphism in telomeric DNA. J Mol Biol 1995; 248:233-8. doi: 10.1016/s0022-2836(95)80046-8 [Crossref] [ Google Scholar]
- Bhattacharyya D, Mirihana Arachchilage G, Basu S. Metal cations in G-quadruplex folding and stability. Front Chem 2016; 4:38. doi: 10.3389/fchem.2016.00038 [Crossref] [ Google Scholar]
- Largy E, Marchand A, Amrane S, Gabelica V, Mergny JL. Quadruplex turncoats: cation-dependent folding and stability of quadruplex-DNA double switches. J Am Chem Soc 2016; 138:2780-92. doi: 10.1021/jacs.5b13130 [Crossref] [ Google Scholar]
- Ma G, Yu Z, Zhou W, Li Y, Fan L, Li X. Investigation of Na + and K + competitively binding with a G-quadruplex and discovery of a stable K + -Na + -quadruplex. J Phys Chem B 2019; 123:5405-11. doi: 10.1021/acs.jpcb.9b02823 [Crossref] [ Google Scholar]
- Tran PL, Mergny JL, Alberti P. Stability of telomeric G-quadruplexes. Nucleic Acids Res 2011; 39:3282-94. doi: 10.1093/nar/gkq1292 [Crossref] [ Google Scholar]
- Tiwari A, Panigrahi SK. HBAT: a complete package for analysing strong and weak hydrogen bonds in macromolecular crystal structures. In Silico Biol 2007; 7:651-61. [ Google Scholar]
- Williamson JR. G-quartet structures in telomeric DNA. Annu Rev Biophys Biomol Struct 1994; 23:703-30. doi: 10.1146/annurev.bb.23.060194.003415 [Crossref] [ Google Scholar]