Bioimpacts. 11(2):87-99.
doi: 10.34172/bi.2021.16
Original Research
A Markov chain-based feature extraction method for classification and identification of cancerous DNA sequences
Amin Khodaei  , Mohammad-Reza Feizi-Derakhshi *
, Mohammad-Reza Feizi-Derakhshi *  , Behzad Mozaffari-Tazehkand
, Behzad Mozaffari-Tazehkand 
Author information:
Faculty of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran
Abstract
Introduction:
In recent decades, the growing rate of cancer incidence is a big concern for most societies. Due to the genetic origins of cancer disease, its internal structure is necessary for the study of this disease.
Methods:
In this research, cancer data are analyzed based on DNA sequences. The transition probability of occurring two pairs of nucleotides in DNA sequences has Markovian property. This property inspires the idea of feature dimension reduction of DNA sequence for overcoming the high computational overhead of genes analysis. This idea is utilized in this research based on the Markovian property of DNA sequences. This mapping decreases feature dimensions and conserves basic properties for discrimination of cancerous and non-cancerous genes.
Results:
The results showed that a non-linear support vector machine (SVM) classifier with RBF and polynomial kernel functions can discriminate selected cancerous samples from non-cancerous ones. Experimental results based on the 10-fold cross-validation and accuracy metrics verified that the proposed method has low computational overhead and high accuracy.
Conclusion:
The proposed algorithm was successfully tested on related research case studies. In general, a combination of proposed Markovian-based feature reduction and non-linear SVM classifier can be considered as one of the best methods for discrimination of cancerous and non-cancerous genes.
Keywords: DNA sequence, Cancer, Classification, Markov chain, Support vector machine
Copyright and License Information
© 2021 The Author(s)
This work is published by BioImpacts as an open access article distributed under the terms of the Creative Commons Attribution License (
http://creativecommons.org/licenses/by-nc/4.0/). Non-commercial uses of the work are permitted, provided the original work is properly cited.
Introduction
The human body is made up of millions of cells which their internal structure plays a vital role in many human features and behaviors. Due to the long length and encoded characteristics of DNA strands, analysis and study of them is an open research challenge. A wide range of analysis methods are proposed by researchers that mainly relied on mathematics, statistics, signal processing and computer algorithms.
1
According to the Ministry of Health reports, cancer is still a terrible genetic disease and results in plenty of deaths worldwide.
2
Cancer is referred to interactions between cell sub-sections. Each cell has several parts in which the most important one is the central nucleus. Human’s nucleus contains 23 pairs of chromosomes. Inside of each chromosome, DNA sequences or deoxyribonucleic acid is located, which is a large molecule that is formed in the shape of a double helix. Consider a DNA molecule in the form of a ladder. Each side of this ladder is made up of sugar-phosphate molecules as shown in Fig. 1.
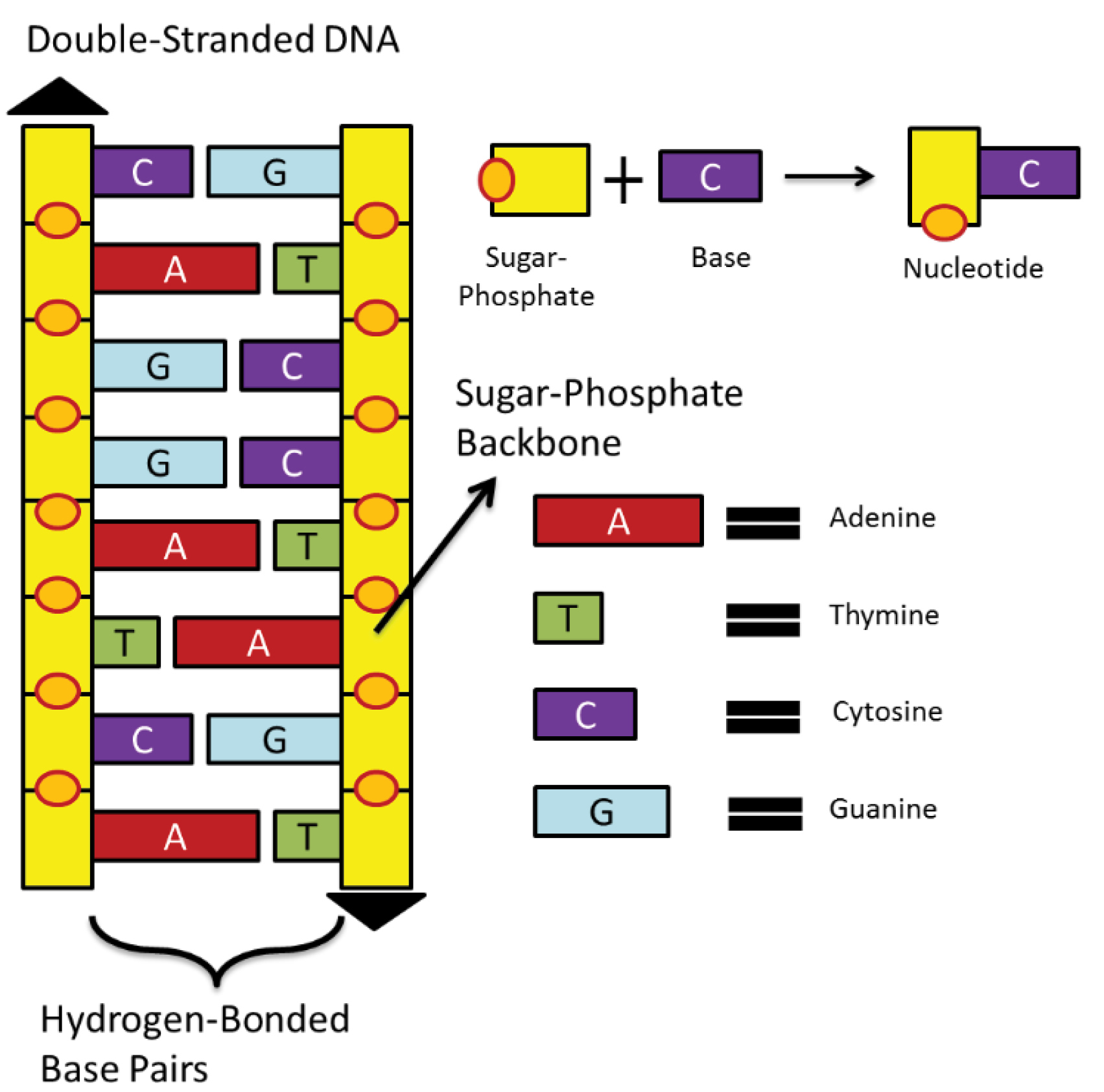
Fig. 1.
Cell structure and its DNA sequence mechanism.
.
Cell structure and its DNA sequence mechanism.
Rungs of this ladder are made up of nitrogen-bases (nucleotides) pairs: Adenine (A), Thymine (T), Cytosine (C), and Guanine (G). Nucleotides complementary nature has the property that always A joins with T and C joins with G nucleotide.
3
Changes in the nucleotides of the DNA sequences, which are known as “mutation”, may lead to genetic diseases. These alterations in the order of nucleotides may affect the corresponding protein sequence. Also, the cause of some genetic diseases may not be just a nucleotide alteration.
3,4
In the past decade, several scientific efforts have been made on mining the DNA sequences. Identification of specific biological patterns (such as locating gene or protein-coding regions) on DNA sequences using signal processing methods are examples of this effort. P. Vaidyanathan and D. Anastassiou’s researches5-7 were the first and most influential studies in this field. Therefore, several studies have been conducted in the field of cancer disease data mining with analysis of DNA sequence protein-coding regions. These types of studies are tested on a set of selected cancerous and non-cancerous genes. Signal processing or other computational approaches have been used for feature extraction. 8- 12
Meanwhile, Satapathi et al
8
report was one of the first studies which analyze cancer DNA sequences by using some custom signal processing techniques, or point out to Das and Barman research that utilizes the capabilities of the Bayesian statistical model for diagnosis of cancer data.
11
For this purpose, some statistical and computational techniques have been explained for feature extraction by distribution frequency concept on amino acid sequences or other computational operators.
13,14
In recent years, different types of researches have been done on sequential data. This has led methods of various science to model or simulate the performance of these sequences. In this regard, Xing et al categorized the sequence type data classification methods in some general parts.
15
One of the newly introduced ideas is the electrical stimulation of the genomic sequence sub-units. Also, Roy et al have succeeded in proving his proposal to various datasets.16-19 One of the positive aspects of this sight was the consideration of DNA sequence units’ chemical structure.
Furthermore, some of the methods suggested a combination of previous approaches idea to improve the performance. Severa studies20-24 have incorporated a combination of signal processing approaches with computational techniques. It is noteworthy that some of these studies have been done on the corresponding amino acid version of genomic sequences, such as Das and Barman.
23
Similar works have been done in this area, such as Roy & Barman, La Rosa et al, and Stepanyan & Petoukhov.
24-26
One of the statistical studies in this field is A. Mesa et al research which has classified genomic sequences by statistical Hidden Markov model.
27
DNA sequences chain construction modeling and gene finding and protein-coding region location prediction are some of the efficient applications which have been studied in recent two decades.
28-31
In the proposed method of this study, the Markov chain has been used in the feature extraction phase.
The main purpose of this research is the structural analysis of genomic sequences in order to distinguish disease-related samples. For this purpose, the genetic features of the samples are extracted as a classification indicator. The above specifications will be further explained in the following sections. The remainder of this paper is organized as follows: Section 2 describes some of the basic concepts and some of the useful tools and algorithms which have been using in the study. In sections 3 and 4, in addition to the described approach, the obtained results are analyzed and presented.
Materials and Methods
In this article, DNA sequences in nucleotide form and their translated protein mapping were analyzed and modeled using computational and statistical methods. In this section, the proposed research applied methods were introduced sequentially. Also, the proposed method and its obtained results were discussed in the third section.In this research, a pattern recognition scheme is proposed for discrimination of cancerous and non-cancerous genes.
The proposed method is a hybrid approach, consisting of the Markov chain-based feature extraction method and support vector machine (SVM) model classifier. In this approach, the Markov chain is used to feature extraction and feature selection purposes, and SVM model classifies the samples based on the selected features. One of the main challenges in the field of genomic research is the different length of case studies. The proposed approach for the feature extraction phase has solved the characteristics of this challenge. The statistical analysis helped to achieve the most effective features from the mentioned features.
In Fig. 2, the basic steps of the proposed algorithm are presented as a flowchart. In this approach, Markov chain is used for feature extraction purposes. After applying an efficient feature selection technique, a non-linear kernel function method has been used for the classification of case studies. Common criteria (such as TP, TN, FP, FN, and accuracy) are also used for evaluation. 10-fold cross-validation is used to improve the proposed model evaluation approach. In the following sections, the methods and techniques will be described in detail.

Fig. 2.
Overall flowchart of the proposed algorithm.
.
Overall flowchart of the proposed algorithm.
Case studies
For evaluation and comparison purposes, sample data were selected from NCBI’s Genbank database.
32
Most of the articles published in the field of DNA sequence classification analyzed at most 20-sample data from this dataset. Furthermore, 200 sample instances are used for the classification of data to evaluate the accuracy of the proposed method. Hundreds of these selected samples are represented non-cancerous cases and similarly hundred instances are cancerous. The selected DNA samples are related to breast cancer genes. The selection of these genes is independent of the human chromosomes position address. This study focuses to analyze DNA sequences and extract specific features in the form of Fasta.
In addition to the mentioned data, the proposed approach has been tested on previous researches sample studies. In the following discussion section, the results of these data will be examined in 704 samples. Table 1 represents the quantitative specifications of case studies in similar earlier articles. In each row of this table, articles reference numbers listed. In some cases, the proposed method has been tested on several kinds of cancer, which are named in the disease column. The number of non-cancerous and cancerous samples is also listed in the “No. of Non-cancerous” and “No. of cancerous” columns, respectively. Also, the last column indicates the sum of the mentioned columns. The last row also contains the sum of these data numbers. It should be noted that some other articles have used the same data for comparative analysis.
9,12,13,17,19,20
Table 1.
Specifications of recent papers case studies
|
Ref.
|
Disease
|
No. of Non-Cancer
|
No. of Cancer
|
Total
|
|
8
|
Breast |
4 |
6 |
10 |
|
16
|
Breast |
9 |
18 |
27 |
| Prostate |
12 |
15 |
27 |
|
11
|
Breast |
7 |
7 |
14 |
| Colon |
7 |
8 |
15 |
| Gastric |
4 |
4 |
8 |
| Prostate |
8 |
4 |
12 |
|
23
|
Breast |
12 |
12 |
24 |
| Colon |
8 |
12 |
20 |
| Prostate |
12 |
11 |
23 |
|
18
|
Colon |
16 |
17 |
33 |
|
24
|
Breast |
19 |
153 |
172 |
| Colon |
16 |
135 |
151 |
| Prostate |
20 |
148 |
168 |
| Total |
Data |
154 |
550 |
704 |
Pattern recognition by sequence mining techniques
The diagnosis of a pattern on a particular data to the classification of them into two or more groups is known as pattern recognition. The data Discrimination criterion is based on the similarities of the extracted features. Pattern recognition has applications in several fields such as designing and modeling smart systems. As Theodoridis and Koutroumbas
33
had written in his book, a pattern recognition model for classifying data has some general steps. The most important steps of a pattern recognition model are feature extraction and feature selection. The next steps of this model are classification design and evaluation. These kinds of systems have training and testing steps. After the training step, the parameters of the proposed model will be computed and can be used for the classification of test data.
33
Markov chain model
Let assume X is a random variable that depends on the independent parameter t, which is usually known as a time parameter. I represent a set of all states (realizations) of a random variable X(t). Family of random variables {X(t), t∈T} with parameter space T, and state-space I is known as a stochastic process. Discrete-time (parameter) stochastic chain is a type of stochastic process in which I and T are finite sets or countable infinite sets. A stochastic process is time-homogeneous if satisfies the following condition
34
:
(1)
Discrete-time Markov chain (DTMC) is a stochastic process that satisfies the following condition
34
:
(2)
The Markovian property states that the conditional probability distribution of the system at the next step depends only on the current state of the system, and not on the state of the system at previous steps. Assume that DTMC is time-homogenous, by considering all states, transition probabilities constitute a squared matrix which is known as a transition matrix. This matrix represents the properties of the internal structure of time-homogeneous DTMC. If the system met some other extra conditions, the steady-state of a system with Markovian property can be computed by using the transition matrix.
34
It has been assumed that a DNA string is a time-homogenous DTMC in which the domain of discrete parameter space T is [0, length (DNA)/3-1] and state-space I belongs to {A, C, G, T}. In this problem, to modeling the first-order Markov chain properties, each nucleotide was assumed as a state in its position. DNA sequences in the nucleotide form (with any length) analyzed by this method. In this approach, the stochastics probability of specific nucleotides after each type of nucleotides is measured separately. Given the number of nucleotide variations, 16 values were calculated for each sample.
The proposed method by considering the protein-coding regions of nucleotide sequences discriminate cancerous samples. The first-order Markov transition matrix is calculated for each pair of nucleotides. For this purpose, the number of observed pairs of nucleotides is computed in a sequential analysis of sample DNA sequences. In this way, the probability distribution of all sixteen pairs of nucleotides considered in each DNA sequence. These sixteen conditional probabilities constitute a transition probability matrix. Our study like other studies indicates that these transition probabilities have Markovian property and we can consider this matrix as a Markovian transition matrix.
The mentioned transition which has been created in our proposed method represents the conditional probability for the appearance of sixteen pairs of nucleotides in a DNA sequence. Elements of this matrix are calculated by equation (3). These values must be normalized. Thus, in this paper group wised normalization is applied to the generated matrix. For this purpose, these sixteen elements of the matrix are categorized into 4 groups such that the first nucleotide for members of each group is the same. Finally, each element of all groups is divided into the sum of the values of its group. As an example, in the 2nd row and 1st column of this matrix, the probability of P(A|C) means the probability of event A given the probability of event C. Similarly other probability values of this matrix calculated one by one.
(3)
This procedure revealed the genomic sequences of chemical units’ patterns in a computational matrix format. This type of normalization makes the transition matrix to be in the form of a Markovian chain’s transition matrix. Based on this type of normalization, the sum of probabilities in each row of the transition matrix will be equal to one. In the final stage, the Markovian transition matrix extracted the discriminative features for the final phases of classification. This procedure is applied to all samples from both cancerous and non-cancerous categories.
In other words, from the pattern recognition modeling perspective, the Markov model is used to feature extraction purposes. Markov chain’s concepts were also influential in the feature selection phase. This issue is facilitated by the use of statistical analysis. Applying the Markov chain model on each sample is summarized as following steps:
-
Getting the nucleotide DNA sequence (Cancerous/ Non-Cancerous)
-
Enumeration of the whole pair of nucleotides, such as AA, CA, GA, … (16 cases)
-
Constitution of a 4*4 matrix, in which each row and column indicates the first and second pairs of nucleotides, respectively.
-
Calculation of conditional probability for each state.
-
Normalizing the matrix for transition matrix computation.
-
Calculation of steady-state for completion of the feature extraction phase.
-
Feature selection by using some statistical analysis like average and standard deviation.
-
In the results section, these steps will be explained by an example. Finally, each sample with its extracted features will be given to the classifier.
Support vector machine
One of the most important parts of each pattern recognition model is the classification scheme. SVM is one of the known classification methods. Its basis is computing hyperplanes with maximum margins for isolating samples in a multidimensional feature space. In the simplest case, SVM can classify multidimensional data that are linearly separable.
Let assume that y= +1 represents cancerous DNA sample data and y= -1 represents a non-cancerous DNA sequence. Dataset D is linearly separable in d-dimensional space if a hyperplane with coefficients w exits that can completely separate two types of samples data in feature space. SVM classification function is in the form of
that sign of (f(x)) represents the class of sample data x. SVM classifies sample data set D as follows:
(4)
Sometimes sample data are not linearly separated. One of the advantages of the SVM method is its applicability in these circumstances. Non-linear decision boundary should be used in the cases that data are not linearly separable. In this situation, data are mapped by a nonlinear function to a new feature space that becomes linearly separated. Then SVM can classify them easily. Several kernel functions have been introduced for this purpose. Each of them is appropriate for specific problems. Some of the known kernel functions are presented in Table 2.
Table 2.
SVM kernel functions
|
Kernel Name
|
Equation
|
| Linear |
|
| Polynomial |
|
| Sigmoid |
|
| RBF |
|
| MLP |
|
Generally, the computation complexity of SVM is high but its capability in discrimination of non-linear dataset, simple training, high generalization and low error rate is its strong advantages.
35,36
It should be noted that there are other types of classifiers in the category of machine learning. The artificial neural network, KNN, decision tree, Bayesian network, and ensemble methods are other efficient techniques in the field of classification. Some of these methods are used in this research (Results section) to compare the performance of the selected approach.
Performance evaluation criteria
One of the most important stages in pattern recognition is the performance evaluation of classification. Four known performance evaluation metrics are True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN). Moreover, other criteria can be derived from the four mentioned primary metrics such as precision, recall, sensitivity, specificity, accuracy, and false alarm. In this study, the accuracy criterion was used to analyze and compare the methods. This criterion is the result of dividing the sum of TP and TN by the sum of all mentioned four metrics.
In pattern recognition classification form, one of the most important and well-known performance evaluation techniques is a validation test. In this technique, data is partitioned into train and test sets. After classification, performance metrics are computed. When a relative number of training data is increased, the generalization power of classification will be decreased. On the other hand, when the relative number of test data is increased, the error estimation of classification will be increased too.
K-Fold cross-validation is one of the most known validation tests, which is also used in this study. In this approach, all data are randomly partitioned into K groups with equal members. One of the mentioned subgroups is considered as a testing set, and the other ones are used as a training set. This process iterates K times and each time one subgroup is chosen as a testing set. Finally, the mean value of K results is considered to be the final result. Generally, the K value is considered to be 10, but it also depends on the number of data and type of the problem.
37,38
Results
It should be noted that the implementation of the proposed method was accomplished in MATLAB software. For example, Fig. 3 displays the probability matrix of the Markov chain for the BRCA2 gene associated sample. In this figure, the transition matrix elements are rounded up to two digits precision. For example, the element of row 2 and column 1 is 0.46 which represents the average probability that A nucleotides appear after C nucleotides.
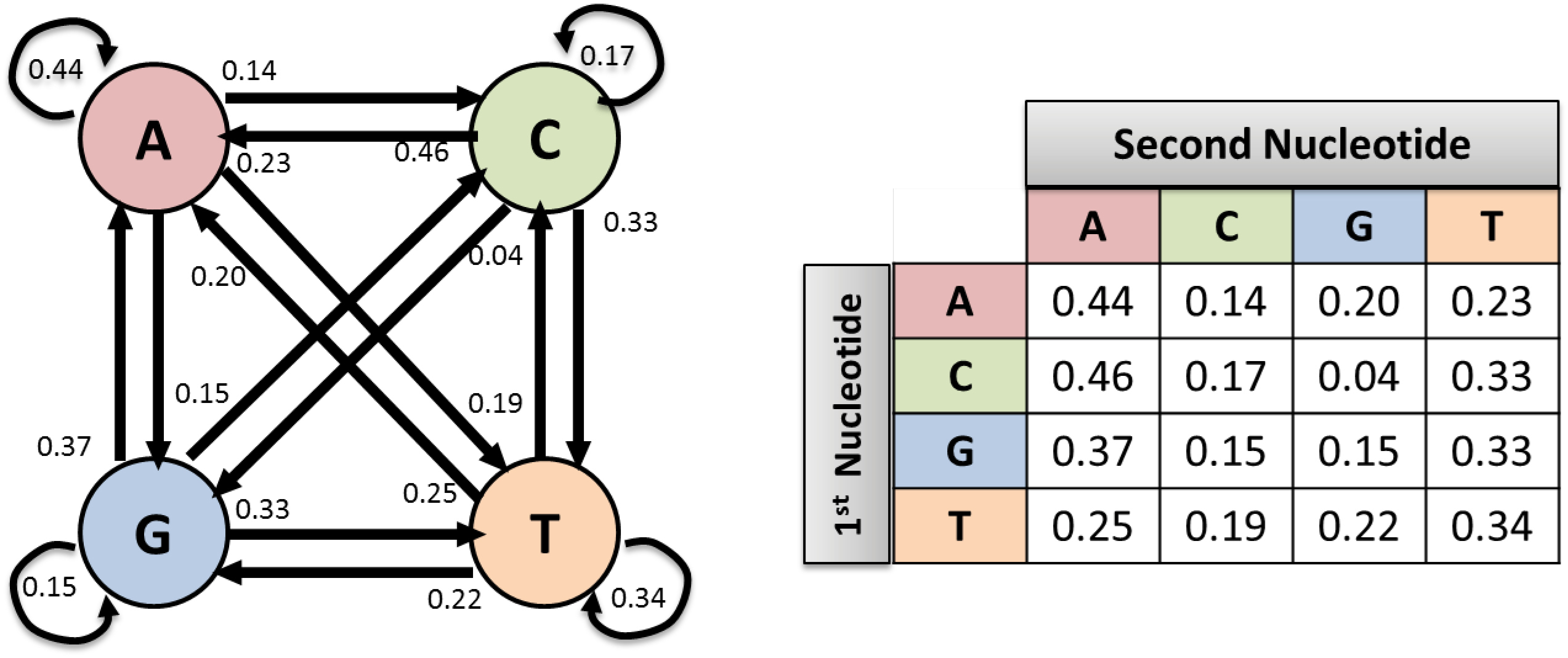
Fig. 3.
Markov chain transition states for BRCA2 cancerous sample gene.
.
Markov chain transition states for BRCA2 cancerous sample gene.
As shown in Fig. 3, the sum of probability in each row has a value of 1. First, the proposed method is applied to the mentioned database for computing transition matrix for all case study samples (cancer and non-cancer). The row-wise representation of the transition matrix can be considered as a feature vector with 16 features. These features can be used for data classification and separation.
Analysis of the obtained matrix indices is effective in the identification of discriminative features. Fig. 4 shows the mean and standard deviation of transition matrix elements’ values of cancer and non-cancerous samples. The horizontal axis of Fig. 4 is divided into four groups in such a way that each group belongs to one of the nucleotides which are appeared as the first element of nucleotide pairs. The vertical axis shows the relative frequency of measured quantities based on the group normalization approach.
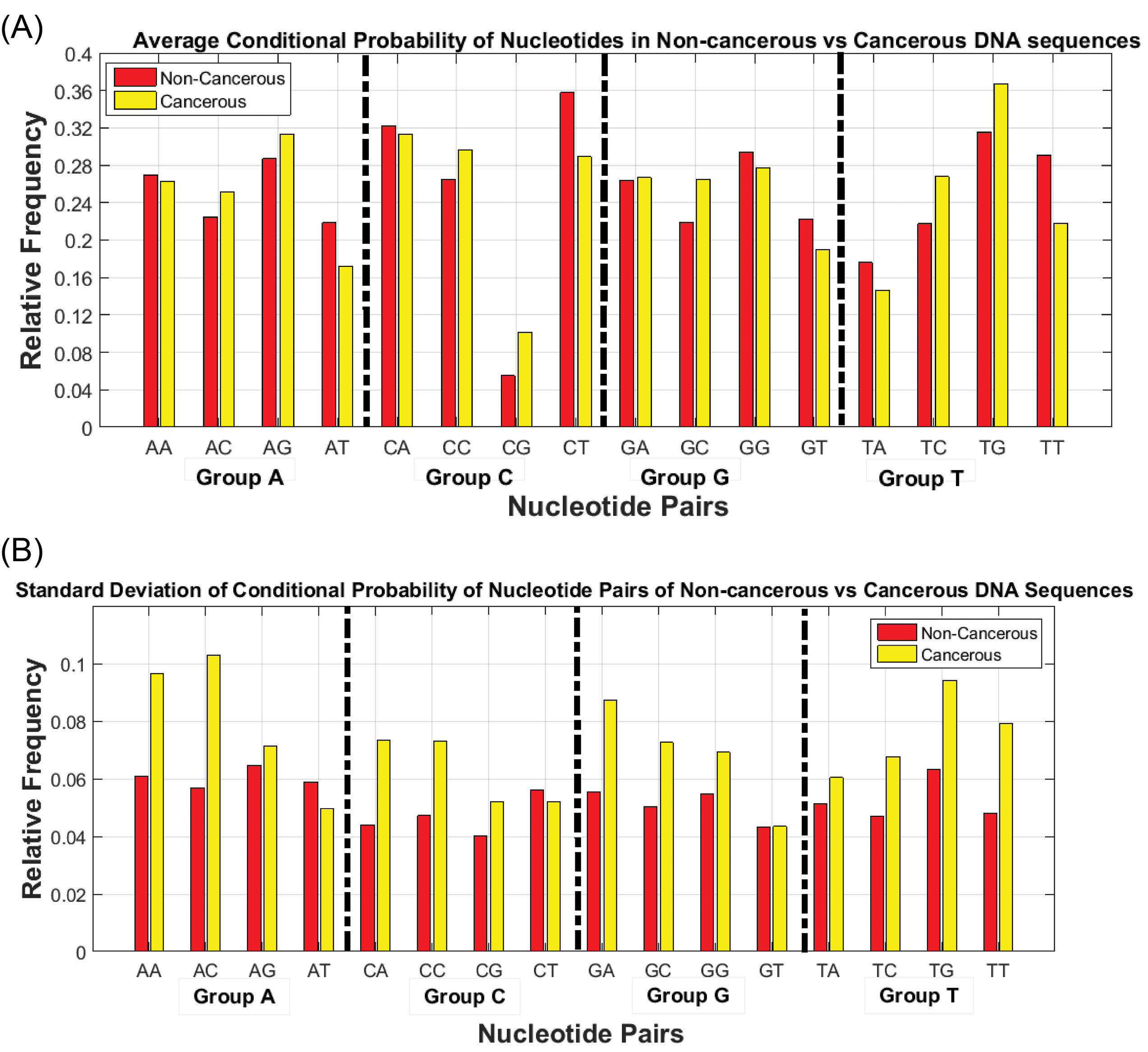
Fig. 4.
Stochastic characteristics of the conditional probability of nucleotide pairs for cancerous and non-cancerous DNA sequences (A) Mean (B) Standard deviation.
.
Stochastic characteristics of the conditional probability of nucleotide pairs for cancerous and non-cancerous DNA sequences (A) Mean (B) Standard deviation.
Fig. 4 shows the values of two statistical metrics for cancerous and non-cancerous DNA sequences which have significant differences. For instance, the probability of observing a special kind of nucleotide binaries such as GT, CT, AT, and TT is higher in non-cancerous samples compared to cancerous samples. Also, the probability of the elements related to TG, TC, and GC in the transfer matrix of cancerous samples is higher than that of non-cancerous samples. In other words, it is possible to define a threshold value that separates cancerous data from non-cancerous ones.
This idea inspires us to propose a preprocessing method that can use this meaningful difference in statistical metrics for discrimination of cancerous and non-cancerous DNA sequences. This technique is performed in two steps: The first step was a dimension reduction procedure in which sequences of thousands of nucleotides are mapped to a feature space with sixteen or lower dimensions. And the second step is related to the discriminative phase in which an appropriate machine learning method is applied for the classification of samples.
Regarding the characteristics of the means and standard deviations that indicate significant differences between cancerous and non-cancerous categories, it can be concluded that using a classifier which exploits these statistical properties can appropriately classify our data. On the other hand, the existing dependency between the features and their non-linear relevancies requires an appropriate method. The SVM classifier benefits these statistical properties in feature space to draw optimal classification hyperplanes. An important point in this step of SVM is selecting an appropriate kernel function that accurately classifies data using available features.
In our experimental studies, SVM classifier with different kernel functions is applied to the feature space of 200 sample DNA sequences. The performance of classifiers is compared with a variety of SVM kernel functions besides some conventional classification techniques. The obtained results are depicted in some figures to compare these methods. The results of Fig. 5 make this comparison in terms of TP, TN, FP, FN criteria. Some of the mentioned SVM’s kernel functions in Table 2 have also been tested in this part. This figure also depicts the classification accuracy that is achieved by different kernel functions. In the following sections, some tests and comparative studies have confirmed the capability of SVM kernel functions in the classification procedure.

Fig. 5.
Comparison of classification methods accuracy in terms of TP, FN, FP, TN metrics.
.
Comparison of classification methods accuracy in terms of TP, FN, FP, TN metrics.
The horizontal axis of Fig. 5 displays the learning approach name for classification. The vertical axis of the figure indicates the percentages of TP, TN, FP, FN metrics for 100 cancerous samples, and 100 noncancerous samples. SVM kernel function capability in the management of non-linear feature space is shown in this figure. The best possible results have been shown by using kernel functions such as polynomial and RBF.
In addition to SVM-based classifiers, several other techniques also have been tested in this figure. Regular versions of artificial neural network (MLP), K-nearest neighbor (KNN), and decision tree (Tree) have also been tested for this purpose. The tested artificial neural network is a feed-forward version with 10 hidden layers and a balanced default weight. The Euclidean distance criterion and 10 neighbors are also considered for the KNN approach parameters. The selected decision tree is also constructed by Gini diversity index. However, there may be some ways to improve the results of these methods by changing its parameters.
Furthermore, Table 3 shows the performance of SVM classification method via different kernel functions in terms of the introduced performance criteria. This comparison is based on the predefined accuracy-based criterion and 10-Fold cross-validation. These criteria are marked with accuracy and performance in this table respectively. It is obvious that increasing the accuracy magnitudes led to more accurate classification results.
Table 3.
Comparison of classification methods in terms of accuracy and 10-Fold criterion
|
Classification method
|
Accuracy
|
Performance
|
| SVM – Linear |
0.86 |
0.72 |
| SVM – Polynomial 2 |
0.97 |
0.87 |
| SVM – Polynomial 3 |
0.98 |
0.90 |
| SVM – Sigmoid |
0.98 |
0.87 |
| SVM – RBF |
1 |
1 |
| ANN – MLP |
0.55 |
0.57 |
| KNN |
0.83 |
0.84 |
| Random forest tree |
0.89 |
0.85 |
The results presented in Table 3 confirmed the results of the previous figure, indicating that the kernel function of polynomial and RBF leads to better classification accuracy. Nevertheless, a method cannot be measured only based on a one-time evaluation of the accuracy-based metrics. It is common practice to use frequent analysis in these conditions in machine learning problems. Thus, in this experiment, the K-Fold approach also has been used for validating the performance of our proposed method. In Table 3, obtained results with 10 times (K = 10) implementation of dimension reduction and classification are depicted. The horizontal axis represents the name of the machine learning technique and its vertical axis represents the accuracy of classification.
Experimental results indicated the low accuracy of the linear kernel function in comparison with other kernel functions. The inappropriate accuracy of the linear kernel functions demonstrated that sample points in new feature space were not linearly separated. Therefore, non-linear classifiers are needed to be used for increased accuracy. Table 3 confirmed the results of the previous figures. Also, it indicates that RBF and polynomial kernel functions have better classification performance compared to other kernel functions.
Discussion
In addition to evaluating the mentioned dataset, the proposed approach is applied to the dataset which is used in similar studies.
8,11,16,18,23,24
The effectiveness of the Proposed method on these data was also discussed in this section. For example, in Fig. 6, the obtained features of the Markov chain are shown. Fig. 6A shows the frequencies of nucleotide pairs for six samples which are cancerous samples and 6B related to the frequencies of four non-cancerous sample genes. The horizontal axis of Fig. 6 illustrates all 16 nucleotide pairs and the vertical axis represents the grouped normalized value of each nucleotide appearance frequencies.

Fig. 6.
A comparison between Satapathi’s samples
8
using the proposed methods obtained from the Markov transition matrix. (A) Cancerous samples (B) Non-cancerous samples.
.
A comparison between Satapathi’s samples
8
using the proposed methods obtained from the Markov transition matrix. (A) Cancerous samples (B) Non-cancerous samples.
Checking each column of Fig. 6 diagrams may not have an impressive consequence. Nevertheless, according to Fig. 6B the transition probabilities of non-cancerous genes in every 16 pairs of nucleotides are relatively similar to cancerous cases. Further, the dispersion of transition probabilities in cancerous genes is interpretable. Due to the genetic mutation nature in cancerous samples, these changes can show increasing or decreasing variations. It is possible to define value or values as a threshold value for each category. It should be noted that obtained results depend on the type of cancer and its associated genes. By focusing on each feature, various analyses and discussions can be performed.
One of the implications of the Markov chain is steady-state vector. Some notable results were obtained by calculating the steady-state of the Markov chain-based obtained matrix. In Fig. 7, the steady-state is computed on Satapathi and colleagues'8 case studies. Given the existing four-dimensional square transition matrix, its steady-state has four elements. These elements characterize the genome constructing nucleotides. The results clearly distinguished between two categories. The probability of corresponding nucleotides in non-cancerous cases was very similar. In addition, the genetic characteristics of the mutual nucleotides in non-cancerous cases were completely observed. On the contrary in cancerous cases, the anomaly was clearly evident.

Fig. 7.
The proposed approach Markov chain method’s obtained from steady-state on Satapathi et al
8
samples.
.
The proposed approach Markov chain method’s obtained from steady-state on Satapathi et al
8
samples.
Another comparative analysis was performed on the
9,16
case studies. Given that these data were related to prostate cancer, it was natural that the obtained values and their defined thresholds were different. After the feature selection phase, the SVM kernel functions classified the obtained feature space. Due to the low number of case studies in these researches, the results of the 100% classification accuracy were easily achieved. Another similar analysis was conducted on Das and Barman study
11
gastric cancer-associated samples. In Fig. 8, the result of the obtained transition matrix on this paper’s DNA sequence protein-coding regions of gastric cancer is shown.
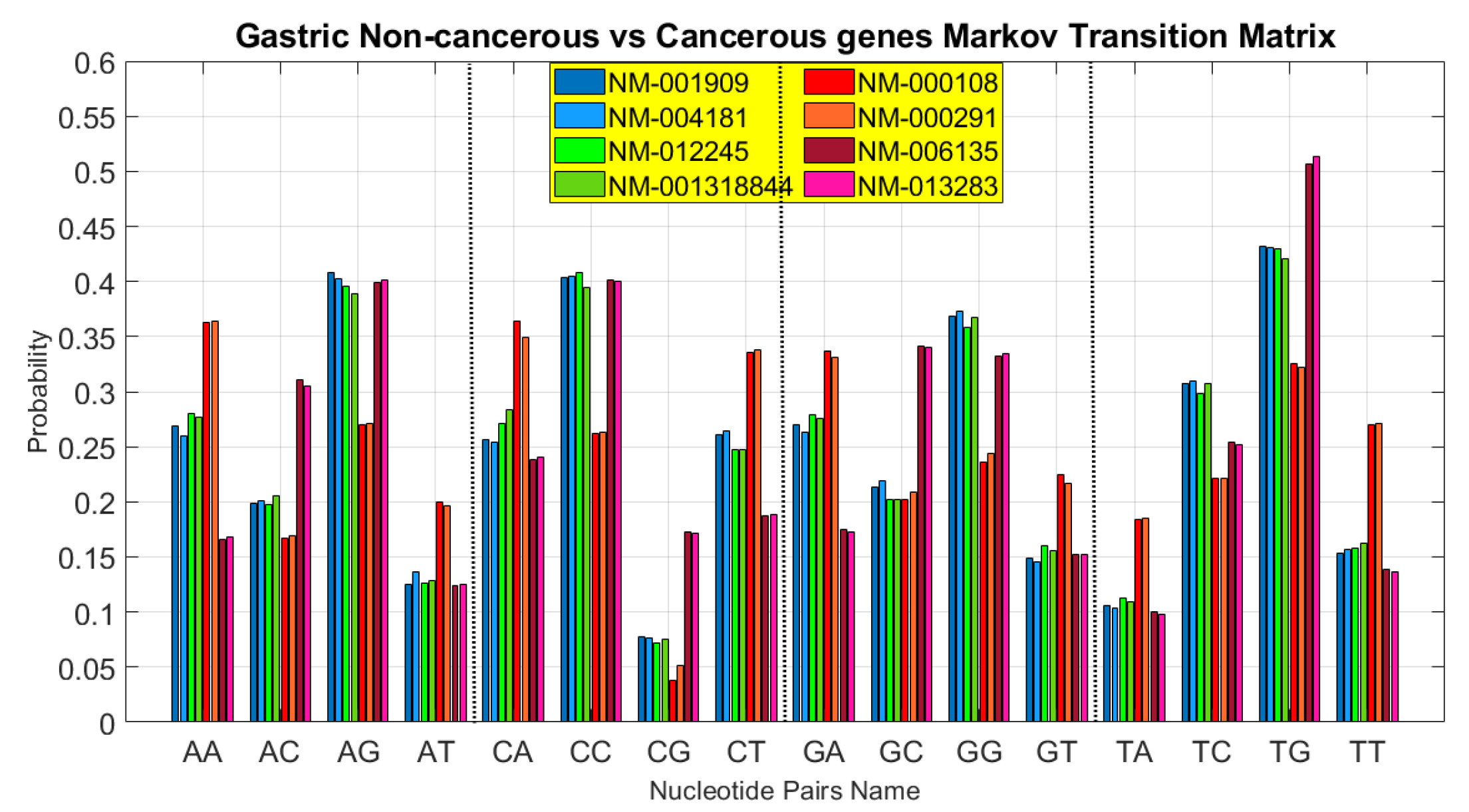
Fig. 8.
Proposed methods’ obtained transition matrix comparison on gastric cancer-associated samples on Das and Barman paper.
11
.
Proposed methods’ obtained transition matrix comparison on gastric cancer-associated samples on Das and Barman paper.
11
In Fig. 8, the horizontal axis indicates the elements of the mentioned matrix in 4 sections. Each section consists of 4 sub-sections. Similar to the preceding figures, the vertical axis represents the probability of each item. Each horizontal axis sub-section consists of 8 bar diagrams, in which the four left-sided cases are non-cancerous and the other ones are cancerous cases. It is also clear that non-cancerous diagrams are much more similar to each other. According to the previous analysis, if the steady-state is calculated in each case study, this significant difference will be apparent.
A similar comparative analysis was carried out on the case studies of several articles.
11,18,23
This analysis is related to the comparison of Markov chain steady-states, depicted in Fig. 9. The first part of this figure (A) is related to the data depicted in the previous figure. The output of the proposed algorithm on the case studies of
18
paper is also confirmed the previous findings in part (B). In part (C) the same diagram is depicted on a series of colon cancer associated genes which were tested in
23
paper. Perhaps compared to the previous charts, the results of this figure did not seem to be distinct. But the use of proper introduced kernel functions in this regard were successful too.

Fig. 9.
Proposed approach Markov chain method’s obtained steady-state on (A) gastric cancer-associated samples of Das and Barman paper
11
(B) colon cancer-associated samples of Bastos et al
14
paper and (C) colon cancer-associated samples of Das and Barman paper.
23
.
Proposed approach Markov chain method’s obtained steady-state on (A) gastric cancer-associated samples of Das and Barman paper
11
(B) colon cancer-associated samples of Bastos et al
14
paper and (C) colon cancer-associated samples of Das and Barman paper.
23
In all parts of Fig. 9, the horizontal axis indicates the accession number of case studies. And the vertical axis represents the percentage of obtained steady state probability. Obtained values similarity of non-cancerous samples and their differences with cancerous cases was apparent in all three sections. This is the result of Markov chain transition matrix described earlier. It should be noted that each part of this figure referred to the genes associated with a particular type of cancer.
Another comparative analysis was done on Roy et al
24
datasets. One of the remarkable points of this research is the number of investigated data. Three different categories of data have been tested in this study. Given the number of data, the effect of the classification method has been examined in this section. In Table 4, a comparison has been made based on the evaluation criteria on prostate cancer-associated sequences. In this figure, part (a) compared the classification techniques in terms of accuracy criterion, and part (b) referred to the 10-Fold cross-validation criterion. In this table, the comparison is based on two predefined criteria.
Table 4.
Comparison of classification methods on [24] prostate cancer-associated sequences in terms of (a) accuracy (b) 10-Fold cross-validation
|
Classification Method
|
Accuracy
|
Performance
|
| SVM – Linear |
0.91 |
0.78 |
| SVM – Polynomial 2 |
0.96 |
0.90 |
| SVM – Polynomial 3 |
0.98 |
0.90 |
| SVM – Sigmoid |
0.96 |
0.90 |
| SVM – RBF |
1.0 |
1.0 |
| ANN – MLP |
0.81 |
0.84 |
| KNN |
0.89 |
0.88 |
| RFT |
0.94 |
0.87 |
The same comparison was successfully made on other datasets of this paper. Fig. 10 is illustrated these results with similar diagrams in 4 sub-sections. The upper (A) and (B) sub-sections referred to breast cancer-associated samples and (C) and (D) sub-sections belonged to colon cancer samples. In parts (A) and (C), the comparison was made according to the accuracy index and other cases compared based on the 10-Fold cross-validation value. The results indicate an improvement in terms of considered criteria by using the SVM–RBF kernel.

Fig. 10.
Comparison of classification methods performance on Roy’s sample
24
(A) accuracy of breast dataset (B) 10-Fold cross-validation of breast dataset (C) accuracy of colon dataset (D) 10-Fold cross-validation of colon dataset.
.
Comparison of classification methods performance on Roy’s sample
24
(A) accuracy of breast dataset (B) 10-Fold cross-validation of breast dataset (C) accuracy of colon dataset (D) 10-Fold cross-validation of colon dataset.
The obtained results and their comparisons with the results of the previous studies demonstrated the successful performance of the proposed approach. As previously proved, the Markov model was successful in modeling the nucleotide components of DNA sequences. In this research, the functionality of the Markov chain was also studied in the modeling of nucleotides order. The implementation of this approach on various gene sequences revealed a distinct result that was successful in genomic data classification. Analysis and comparisons were not conducted on a specific type of cancer. Some of the efficient genes in breast, prostate, and colon cancer were analyzed in this research.
On the other hand, the results of cancerous cases confirmed the genetic nature of gene mutation. Since the cancer is formed by a nucleotide (or multi-nucleotide) mutation, a minor change in DNA sequence cause big impression formation and diffusion of cancerous cell. It should be noted that some genes which are known to be effective in developing breast cancer, also affect the formation and growth of other genetic diseases. The importance of sequencing and reading DNA sequences should not be neglected, since a small error at these stages could influence the subsequent analysis and processing.
The results emphasize the high-accuracy and completeness of a non-linear classification is more than other methods like previously reported results. The similarity of non-cancerous features to each other and the standard deviation of these features on cancerous case features were effective in designing classifiers. The proposed classification method used the obtained features which greatly reduces computational overhead compared to the classification was applied on the DNA sequences with high feature dimension. Experimental results showed that the proposed feature dimension reduction method does not decrease the accuracy of classification.
One of the advantages of the proposed approach is considering the DNA sequences unit interactions. This issue is made by using the Markov chain-based feature extraction method. The results have revealed a significant relationship between the extracted features. In addition to verifying the discrimination of cancerous samples, these features are inferable from a genetic and chemical perspective. This approach can also be modeled in the prediction and identification of cancerous genomic sequences. One of the advantages of the proposed method is the use of fewer features. This can also improve classification performance.
Furthermore, there is no mapping, coding, signal processing, simulation, or electrical modeling approach. This has led to one of the benefits of the proposed method, which is performance speed and computational complexity. The proposed approach successfully has been tested on several datasets of cancer types. This also contributes to the high generalizability of the algorithm. In other words, one of the other advantages of the proposed method is not a limitation of specific types of cancer or involved genes. This issue has also been tested in some other research in this area, but most of them have not been properly compared with previous works. In previous researches, only the feature values of the samples considered and the classification phase is not included. One of the advantages of this research is a comparative analysis of its requirements versus similarly accomplished researches.
Conclusion
Cancer is one of the deadly diseases, demands a more thorough investigation. Due to the importance of the subject, other science researchers have also been eager for this subject. Specific data mining techniques and computational statistic approaches beyond usual ones are required to analyze DNA sequences, because of their large volume of information. In this paper, protein-coding regions of DNA sequences are explored by computational and statistical methods, in the form of sequential pattern mining of genes to reveal similarities and differences between cancerous and non-cancerous DNAs.
A novel hybrid method is presented in this paper for discrimination of cancerous DNA genes from non-cancerous ones. As a case study, analysis is performed on breast cancer’s DNAs. The proposed method is based on the combination of new feature mapping and non-linear SVM methods. Related studies have shown that the appearance probability of two pairs of nucleotides in the DNA sequence has Markovian property. This fact is exploited in the first step of our proposed method for feature selection purposes. Then, group-based normalization of yielded features in DNA sequences protein-coding regions is performed successfully. Results show that new reduced feature space with sixteen (or even four) dimensions can discriminate cancerous and non-cancerous DNA samples with very high accuracy.
The experimental results have been indicated that non-linear SVM with polynomial or RBF kernel functions yielded more accurate results for discrimination of cancerous and non-cancerous genes in comparison with other kernel functions. Classification accuracy of the proposed method on breast cancer samples for classifying 200 samples with 100 cancerous and 100 non-cancerous DNA samples yield 100% accuracy. The proposed method has low computational overhead in comparison with similar methods.
Acknowledgment
None to declared.
Funding sources
This research did not receive any specific grant from funding agencies.
Ethical statement
The authors declare that they have no ethical statement.
Competing interests
The authors declare that they have no conflict of interests.
Authors' contribution
This work was carried out in collaboration between all authors. AKH and BMT drafted the manuscript. AKH and MFD developed the analysis. All authors read and approved the final manuscript.
Research Highlights
What is the current knowledge?
simple
-
√ Importance of genomic sequence analysis in order to distinguish disease-related samples.
-
√ Difference length of case studies in terms of nucleotide numbers.
What is new here?
simple
-
√ For the first time, a hybrid Markov chain and SVM-based technique was used for the classification of genomic sequences.
-
√ The proposed approach is not limited to specific types of cancer or involved genes.
-
√ Low complexity and memory of applied methods tackled the challenge of high dimension.
References
-
Xiong J. Essential bioinformatics: Cambridge University Press; 2006. 10.1017/CBO9780511806087
- Somi M, Mousavi S, Rezaeifar P, Naghashi S. Cancer incidence among the elderly population in the northwest of Iran: a population based study. Iranian J Cancer Prev 2009; 2:117-26. [ Google Scholar]
-
Alberts B. Molecular biology of the cell. 5th ed. Garland Science; 2008. 10.1002/bmb.20192
-
Pecorino L. Molecular Biology of Cancer: Mechanisms, Targets, And Therapeutics. Oxford University Press; 2012.
- Vaidyanathan P. Genomics and proteomics: A signal processor's tour. IEEE Circuits and Systems Magazine 2004; 4:6-29. doi: 10.1109/MCAS.2004.1371584 [Crossref] [ Google Scholar]
- Vaidyanathan P, Yoon B-J. The role of signal-processing concepts in genomics and proteomics. J Franklin Inst 2004; 341:111-35. doi: 10.1016/j.jfranklin.2003.12.001 [Crossref] [ Google Scholar]
- Anastassiou D. Genomic signal processing. IEEE Signal Process Mag 2001; 18:8-20. doi: 10.1109/79.939833 [Crossref] [ Google Scholar]
- Satapathi G, Srihari P, Jyothi A, Lavanya S, editors editors. Prediction of cancer cell using DSP techniques 2013. International Conference on Communication and Signal Processing 2013; 149:153. doi: 10.1109/iccsp.2013.6577034 [Crossref] [ Google Scholar]
- Ghosh A, Barman S. Prediction of prostate cancer cells based on principal component analysis technique. Procedia Technology 2013; 10:37-44. doi: 10.1016/j.protcy.2013.12.334 [Crossref] [ Google Scholar]
- Murugan NSV, Vallinayagam V, Kannan KS, Viveka T. Analysis of liver cancer DNA sequence data using data mining. Int J Comput Appl 2013; 61:6. [ Google Scholar]
-
Das J, Barman S. Bayesian fusion in cancer gene prediction. Int J Comput Appl 2014; 5-10.
- Ghosh A, Barman S. Realization of an EVD model in LabView environment for identification of cancer and healthy homo sapeins genes. Annals of the Faculty of Engineering Hunedoara 2015; 13:195. [ Google Scholar]
-
Barman S, Saha S, Mondal A, Roy M, editors. Signal processing techniques for the analysis of human genome associated with cancer cells. 2nd annual IEEE Information Technology, Electronics and Mobile Communication Conference; 2011; 570-573.
- Bastos CA, Afreixo V, Pinho AJ, Garcia SP, Rodrigues JM, Ferreira PJ. Inter-dinucleotide distances in the human genome: an analysis of the whole-genome and protein-coding distributions. J Integr Bioinform 2011; 8:31-42. doi: 10.2390/biecoll-jib-2011-172 [Crossref] [ Google Scholar]
- Xing Z, Pei J, Keogh E. A brief survey on sequence classification. SIGKDD Explor 2010; 12:40-8. doi: 10.1145/1882471.1882478 [Crossref] [ Google Scholar]
- Roy T, Barman S. A behavioral study of healthy and cancer genes by modeling electrical network. Gene 2014; 550:81-92. doi: 10.1016/j.gene.2014.08.020 [Crossref] [ Google Scholar]
- Roy T, Barman S. Design and development of cancer regulatory system by modeling electrical network of gene. Microsyst Technol 2016; 22:2641-53. doi: 10.1007/s00542-015-2548-x [Crossref] [ Google Scholar]
- Roy T, Barman S. Performance analysis of network model to identify healthy and cancerous colon genes. IEEE J Biomed Health Inform 2015; 20:710-6. doi: 10.1109/JBHI.2015.2408366 [Crossref] [ Google Scholar]
- Roy T, Barman S. Modeling of cancer classifier to predict site of origin. IEEE Trans Nanobioscience 2016; 15:481-7. doi: 10.1109/TNB.2016.2573319 [Crossref] [ Google Scholar]
- Ghosh A, Barman S. Application of BT and PC-BT in Homo sapiens gene prediction. Microsyst Technol 2016; 22:2691-705. doi: 10.1007/s00542-015-2573-9 [Crossref] [ Google Scholar]
- Dakhli A, Bellil W. Wavelet neural networks for DNA sequence classification using the genetic algorithms and the least trimmed square. Procedia Comput Sci 2016; 96:418-27. doi: 10.1016/j.procs.2016.08.088 [Crossref] [ Google Scholar]
- Mariapushpam IT, Rajagopal S. Improved algorithm for the detection of cancerous cells using discrete wavelet transformation of genomic sequences. Curr Bioinform 2017; 12:543-50. doi: 10.2174/1574893611666160712222525 [Crossref] [ Google Scholar]
- Das J, Barman S. DSP based entropy estimation for identification and classification of Homo sapiens cancer genes. Microsyst Technol 2017; 23:4145-54. doi: 10.1007/s00542-016-3056-3 [Crossref] [ Google Scholar]
- Roy SS, Barman S. A non-invasive cancer gene detection technique using FLANN based adaptive filter. Microsyst Technol 2021; 27:463-78. doi: 10.1007/s00542-018-4036-6 [Crossref] [ Google Scholar]
- La Rosa M, Fiannaca A, Rizzo R, Urso A. Probabilistic topic modeling for the analysis and classification of genomic sequences. BMC Bioinformatics 2015; 16:S2. doi: 10.1186/1471-2105-16-S6-S2 [Crossref] [ Google Scholar]
- Stepanyan I, Petoukhov S. The matrix method of representation, analysis and classification of long genetic sequences. Information 2017; 8:12. doi: 10.3390/info8010012 [Crossref] [ Google Scholar]
- Mesa A, Basterrech S, Guerberoff G, Alvarez-Valin F. Hidden Markov models for gene sequence classification. Pattern Anal Appl 2016; 19:793-805. doi: 10.1007/s10044-015-0508-9 [Crossref] [ Google Scholar]
- Henderson J, Salzberg S, Fasman KH. Finding genes in DNA with a hidden Markov model. J Comput Biol 1997; 4:127-41. doi: 10.1089/cmb.1997.4.127 [Crossref] [ Google Scholar]
- Burge CB, Karlin S. Finding the genes in genomic DNA. Curr Opin Struct Biol 1998; 8:346-54. doi: 10.1016/S0959-440X(98)80069-9 [Crossref] [ Google Scholar]
- Choo KH, Tong JC, Zhang L. Recent applications of hidden Markov models in computational biology. Genomics Proteomics Bioinformatics 2004; 2:84-96. doi: 10.1016/s1672-0229(04)02014-5 [Crossref] [ Google Scholar]
- De Fonzo V, Aluffi-Pentini F, Parisi V. Hidden Markov models in bioinformatics. Curr Bioinform 2007; 2:49-61. doi: 10.2174/157489307779314348 [Crossref] [ Google Scholar]
-
GenBank National Center for Biotechnology Information Database. Available from: http://www.ncbi.nlm.nih.gov.
-
Theodoridis S, Koutroumbas K. Pattern recognition. 2003. Elsevier Inc; 2009. 10.1016/B978-1-59749-272-0.X0001-2
-
Grinstead CM, Snell JL. Introduction to Probability. American Mathematical Society; 2012.
-
Shawe-Taylor J, Cristianini N. Kernel methods for pattern analysis. Cambridge University Press; 2004. 10.1017/CBO9780511809682
-
Amami R, Ayed DB, Ellouze N. An empirical comparison of SVM and some supervised learning algorithms for vowel recognition. arXiv preprint arXiv:150706021 2015.
-
Han J, Pei J, Kamber M. Data mining: concepts and techniques: Elsevier; 2011. 10.1016/C2009-0-61819-5
-
Dong G, Pei J. Classification, clustering, features and distances of sequence data. Sequence data mining: Springer; 2007; 47-65. 10.1007/978-0-387-69937-0_3